Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 9 Answered

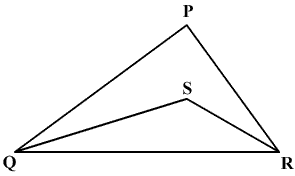
if AB=CB, AB=CD, and EF bisects BD at G .prove that G is mid point of EF.
Asked by vaibhavmishratempleton | 22 Aug, 2014, 11:25: PM
answered-by-expert Expert Answer
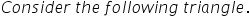
C o n s i d e r space t h e space f o l l o w i n g space t r i a n g l e.
F r o m space t h e space f i g u r e comma space i t space i s space c l e a r space t h a t space A B C D space i s space a space r e c tan g l e space a n d space sin c e space A B equals B C equals C D comma space i t space i s space c l e a r space t h a t space A B C D space i s space a s q u a r e. S i n c e space v e r t i c a l l y space o p p o s i t e space a n g l e s space a r e space e q u a l ; comma space w e space h a v e comma angle D G E equals angle B G F G i v e n space t h a t space E F space b i s e c t s space B D space a t space G. rightwards double arrow D G equals B G T h e space d i a g o n a l space B D space i s space a space t r a s v e r s a l space b e t w e e n space t h e space p a r a l l e l space l i n e s space A B space a n d space C D space a n d space h e n c e a l t e r n a t e space i n t e r i o r space a n g l e s space a r e space e q u a l. rightwards double arrow angle B D C equals angle A B D T h u s comma space b y space A n g l e minus S i d e minus A n g l e space c r i t e r i o n space o f space c o n g r u e n c e comma space w e space h a v e comma triangle B F G approximately equal to triangle D E G. T h u s comma space b y space t h e space p r o p e r t y comma space c o r r e s p o n d i n g space p a r t s space o f space t h e space c o r r e s p o n d i n g space t r i a n g l e space a r e space e q u a l comma space w e space h a v e comma E G equals F G rightwards double arrow G space i s space t h e space m i d p o i n t space o f space E F
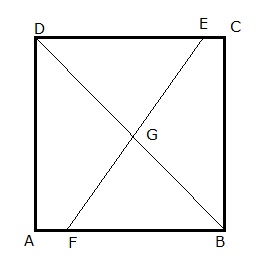
Answered by Vimala Ramamurthy | 25 Aug, 2014, 09:01: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 9 - Maths
prove that medians of a triangle are equal
Asked by kandalashyamala20 | 27 Dec, 2022, 02:30: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
show that in a right angle triagle the hypotenuse is the longest side
question image
Asked by khardewsawrudolf | 22 May, 2020, 02:34: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
What is the greatest possible perimeter of a right angeled triangle with integer sides lengths if one of the sides has length 12?
Asked by vikasg13.hardware | 13 Jun, 2018, 12:01: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 10:05: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that the perimeter of a triangle is greater than the sum of its three medians.
Asked by Topperlearning User | 11 Aug, 2017, 08:45: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that if two sides of a triangle are unequal, the longer side has greater angle opposite it.
Asked by Topperlearning User | 11 Aug, 2017, 08:47: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
In the figure PQ > PR, QS and RS are the bisectors of Q and R respectively. Prove that SQ > SR.
Asked by Topperlearning User | 11 Aug, 2017, 08:47: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that the sum of the three altitudes of a triangle is less than the sum of the three sides of the triangle.
Asked by Topperlearning User | 11 Aug, 2017, 10:06: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
In the figure AD is the bisector of A, prove that AB > BD.
Asked by Topperlearning User | 11 Aug, 2017, 10:04: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
In the given figure, x > y. Show that LM > LN.
Asked by Topperlearning User | 11 Aug, 2017, 08:40: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×