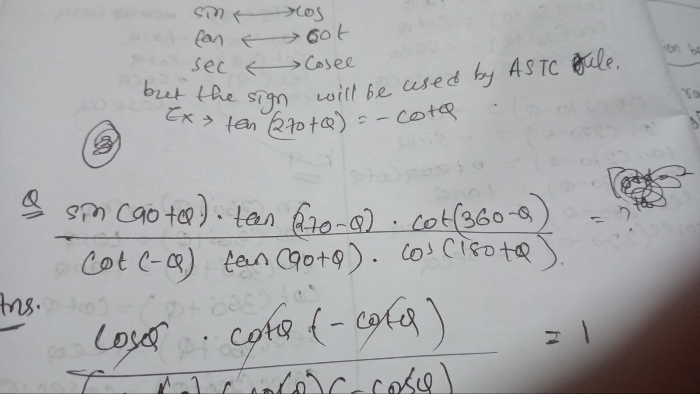CBSE Class 11-science Answered

Dear Student,

Let us find the minimum and maximum values of sinx ± cosx.

y = sin(x) + cos(x)

dy/dx = cos(x) - sin(x)

Now, you make dy/dx = 0.

0 = cos(x) - sin(x)

Move sin(x) to the left hand side.

sin(x) = cos(x)

Divide both sides by cos(x).

sin(x)/cos(x) = 1
tan(x) = 1
x = { pi/4 + k×pi | k an integer }

So we have an infinite number of critical values. Since this is periodic and repeats every pi times, and pi is half a circle, all we need to use is two consecutive values.
Let's try pi/4, 5pi/4.

If x = pi/4, then
y = sin(pi/4) + cos(pi/4)
= √ (2)/2 + √ (2)/2
= 2√ (2)/2
= √ (2)

If x = 5pi/4, then
y = sin(5pi/4) + cos(5pi/4)
y = -√ (2)/2 + -√ (2)/2
y = -√ (2)

So,

-√2  ≤ sin(x) + cos(x) ≤ √2

In general, if we follow similar steps, it comes out that

-√(p²+q²) ≤ psin(x) ± qcos(x) a ≤ √(p²+q²)

Hence, in the given problem,

a ≤ 3sin(A - Π/6) + 2 cos(A + Π/3) ≤ b

=> a ≤ 3sin[Π - (A - Π/6)] + 2 cos(A + Π/3) ≤ b

=> a ≤ 3sin(A + Π/3) + 2 cos(A + Π/3) ≤ b

=> a = -√(3² + 2²) and b = √(3² + 2²)

=> a = -√13 and b = √13

=> a+b =0

Regards Topperlearning.