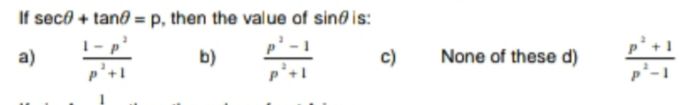CBSE Class 10 Answered
- If A be the area of a right triangle and x is one of the sides containing right angle .Prove that the length of altitude on the hypotenuse is 2Ax / √(x^2 +4A^2).
Asked by sucharitasahoo1 | 24 Nov, 2017, 06:04: PM

Answered by Arun | 24 Nov, 2017, 07:07: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by mraniruddha03 | 02 Apr, 2024, 06:44: PM
CBSE 10 - Maths
Asked by priyanshdhiman2008 | 25 Dec, 2023, 03:12: PM
CBSE 10 - Maths
Asked by deepakverma786024 | 18 Dec, 2022, 05:43: AM
CBSE 10 - Maths
Asked by Bavashreelogasundaram | 22 Sep, 2022, 08:26: PM
CBSE 10 - Maths
Asked by sahanahosamani2005 | 25 Nov, 2020, 10:58: PM
CBSE 10 - Maths
Asked by choudharylakshay786 | 16 May, 2020, 12:56: PM
CBSE 10 - Maths
Asked by kssvsv2011 | 09 May, 2020, 08:44: PM
CBSE 10 - Maths
Asked by gurunath196107 | 07 Apr, 2020, 04:21: PM