CBSE Class 10 Answered

If the area of the triangle formed by joining the given points is zero, then the points will be collinear.

Here, x₁ = a, y₁ = a²; x₂ = b, y₂ = b²; x₃ = c, y₃ = c²

Substituting the values in the formula, we get,

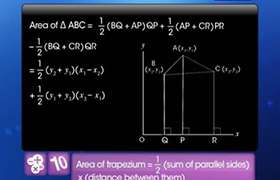
Area of triangle =

= [ab² - ac² + bc² - a²b + a²c - cb²]

= [-a² (b - c) + a (b² - c²) - bc (b - c)]

= [(b - c) {-a² + a (b + c) - bc}]

= [(b - c) (-a² + ab + ac - bc)]

= [(b - c) {a(-a + b) + c(a - b)]

= [(b - c) (a - b) (c - a)]

It is given that a b c, therefore, area of the triangle 0

Hence, the given points can never be collinear.