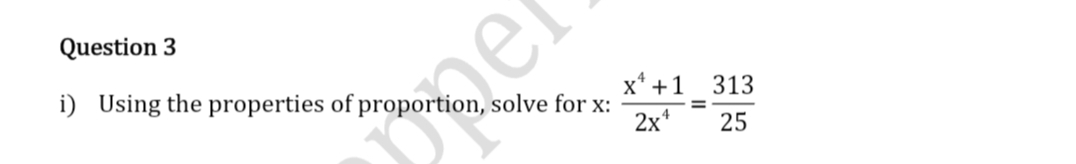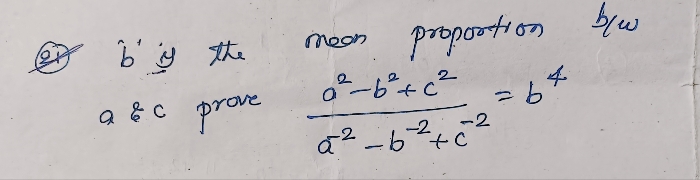ICSE Class 10 Answered
If a, b,c,d are in continued proportion prove that
(a-b)^3 / (b-c)^3= a/d
Asked by arorasweety557 | 20 May, 2020, 02:16: PM
Expert Answer
a, b, c, d are in continued proportion
Therefore, we have
a/b = b/c = c/d = k (say)
c=dk, b=ck=dk2, a=bk=dk3
Consider,
(a-b)3 : (b-c)3
= (dk3 - dk2)3 : (dk2 - dk)3
= d3k6(k - 1) : d3k3(k - 1)
= k3
a/d = dk3/d = k3
Hence, (a-b)3 : (b-c)3 = a : d
Answered by Renu Varma | 20 May, 2020, 07:13: PM
Concept Videos
-
Ratio and Proportion
Ratio and Proportion, Proportions
ICSE 10 - Maths
Asked by vrj.parmar369 | 07 Mar, 2024, 11:27: AM
ANSWERED BY EXPERTICSE 10 - Maths
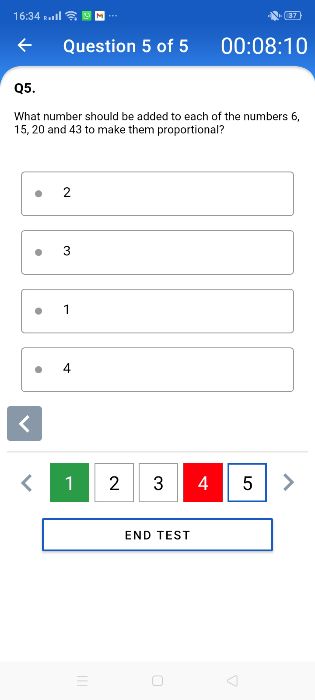
Asked by ng028277 | 27 Jan, 2024, 07:36: PM
ANSWERED BY EXPERTICSE 10 - Maths
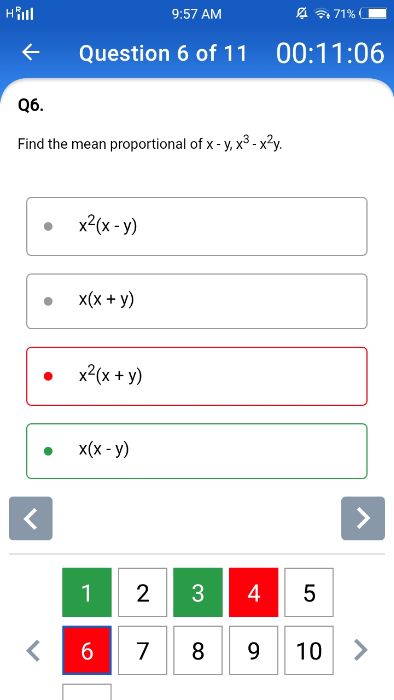
Asked by kalayani822 | 09 Oct, 2023, 08:25: AM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by nehalmukhia53 | 21 Jun, 2022, 07:46: PM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by shaikazheruddin245 | 16 Feb, 2022, 02:50: PM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by harendrapratapsingh8858 | 18 Nov, 2021, 04:34: PM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by anumatiravi14 | 30 Sep, 2021, 10:09: AM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by brijt66 | 05 Aug, 2021, 06:28: AM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by umeshkumargouda1 | 16 Jun, 2021, 07:15: PM
ANSWERED BY EXPERT
