CBSE Class 10 Answered
If A+B+C=90° and cosA=cosB×cosC then show that tanB +tanC= 1
Asked by akankshibhattacharjee4 | 24 May, 2014, 02:00: PM

Answered by Vimala Ramamurthy | 26 May, 2014, 11:39: AM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by ankitakulhar075 | 03 Apr, 2022, 08:43: PM
CBSE 10 - Maths
Asked by arunpattu22 | 11 Jun, 2021, 11:21: AM
CBSE 10 - Maths
Asked by debasreepartha | 23 Apr, 2021, 08:38: AM
CBSE 10 - Maths
Asked by lavanyasureshkumar | 24 Aug, 2020, 04:02: PM
CBSE 10 - Maths
Asked by meenakshisrinivas4 | 20 Apr, 2020, 12:10: PM
CBSE 10 - Maths
Asked by Maharanam446 | 22 Jan, 2020, 01:21: PM
CBSE 10 - Maths
Asked by sadhanapatil494 | 13 Jan, 2020, 08:02: PM
CBSE 10 - Maths
Asked by preetisonips22 | 04 Jan, 2020, 05:44: PM
CBSE 10 - Maths
Asked by shethdhrumil0 | 20 Dec, 2019, 12:09: AM







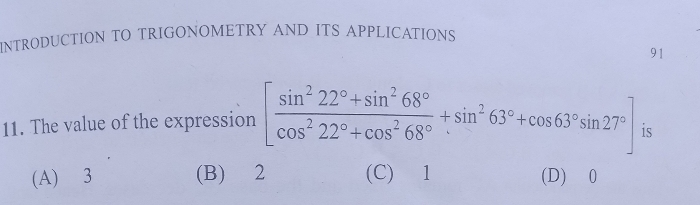
 ABC, then sin2 A + sin2 B =
ABC, then sin2 A + sin2 B =