CBSE Class 9 Answered
how to solve root 10 and 7.3 on number line
Asked by gaurav72001 | 17 May, 2014, 03:22: PM
Expert Answer
Consider a number line. Let the point O represent 0 and point A represent 3.
Now draw a perpendicular AP at A on the number line and cut off arc AB = 1 unit.
Using Pythagoras Theorem, we have
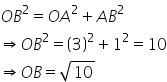
With O as the centre and 
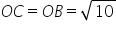as radius draw an arc cutting real line at C. Clearly, 
.
as radius draw an arc cutting real line at C. Clearly, 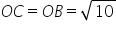.Thus, C represents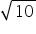 
on the number line.
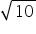on the number line.Now let us find the square root of 7.3
Make a list of perfect squares, 0, 4, 9, 16, 25, 36, ....
Identify perfect squares closest to 7.3
Thus we have, 4 < 7.3 < 9
Take a positive square root of each number.
Thus, we have 
Now evaluate the square roots.
Therefore, we have,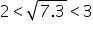 
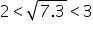
Now make a list of perfect squares between 2 and 3.
| Numbers | Squares |
| 2.1 | 4.41 |
| 2.2 | 4.84 |
| 2.3 | 5.29 |
| 2.4 | 5.76 |
| 2.5 | 6.25 |
| 2.6 | 6.76 |
| 2.7 | 7.29 |
| 2.8 | 7.84 |
| 2.9 | 8.41 |
Thus, from the list it is clear that, 7.29 is closer to 7.3.
Therefore, we have,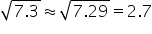 
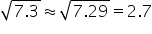
Thus, we can mark 2.7 on the number line as follows:
Thus, OA represents the square root of 7.3
Answered by Vimala Ramamurthy | 21 May, 2014, 10:02: AM
Concept Videos
-
Representation on Number Line
This video covers examples on graphical representation of whole numbers, in... -
Representation on Number Line
Graphical representation of whole numbers, integers, rational numbers and i... -
Representation on Number Line
Graphical representation of whole numbers, integers, rational numbers and ...
CBSE 9 - Maths
Asked by jasaswinimallik | 04 Apr, 2022, 08:54: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by shyammanoharjaiswal | 20 Jul, 2021, 08:12: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by anilgupta9542 | 18 Aug, 2020, 02:41: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by pandeyruby250 | 05 Jun, 2020, 07:24: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by sarvankumar9124 | 06 May, 2020, 10:40: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by Jaiwanthsiva | 04 May, 2020, 07:53: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by Nimmi | 25 Apr, 2020, 01:38: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by ajaypathak.ko | 10 Apr, 2020, 08:59: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by srikantmpai | 05 Mar, 2020, 09:31: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by dikshathakur1272005 | 29 Feb, 2020, 10:57: AM
ANSWERED BY EXPERT
