Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

How to prove `ratio of corresponding sides of similar triangles is equal to ratio of their perimeters` ?
Asked by Sanjay | 15 Aug, 2014, 10:39: AM
answered-by-expert Expert Answer
Consider two triangles ABC and PQR.
S i n c e space triangle A B C space a n d space triangle P Q R space a r e space s i m i l a r space t r i a n g l e s comma space w e space h a v e fraction numerator A B over denominator P Q end fraction equals fraction numerator B C over denominator Q R end fraction equals fraction numerator A C over denominator P R end fraction equals k T h u s comma space space w e space h a v e comma fraction numerator A B over denominator P Q end fraction equals fraction numerator B C over denominator Q R end fraction equals fraction numerator A C over denominator P R end fraction equals fraction numerator k P Q plus k Q R plus k P R over denominator P Q plus Q R plus P R end fraction equals fraction numerator k open parentheses P Q plus Q R plus P R close parentheses over denominator P Q plus Q R plus P R end fraction equals fraction numerator P e r i m e t e r space o f space triangle A B C over denominator P e r i m e t e r space o f space triangle P Q R end fraction
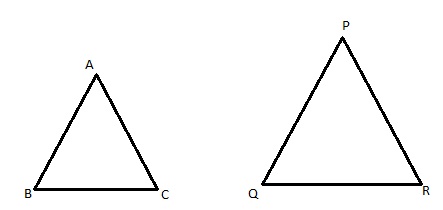
Answered by Vimala Ramamurthy | 16 Aug, 2014, 02:56: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
the perimeter of two similar triangles are 25cm and 15cm respectively. if one side of the first triangle is 9cm,what is the corresponding side of the other triangle
Asked by bhu.joshi54 | 16 Jun, 2022, 07:56: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Question is in image
question image
Asked by psinghaladv | 05 Oct, 2021, 07:49: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Ta^2 30+cot^2 30 =10/3 is this true or false
Asked by akssrhsundaram | 27 Sep, 2021, 07:17: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
One day Rahul decided to measure the height of the building in his locality. He is 5 feet tall. He places a mirror on the ground and moves until he can see the top of the building. At the instant when Rahul is 2 feet from the mirror, the building is 48 feet from the mirror. Find 1. The Height of the building. (A.120, B.96, C.40, D.180)
question image
Asked by bassichtmlpage | 26 Mar, 2021, 10:18: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
A right circular cone is divide by a plane parallel to its base into two equal volume.In what ratio the height of the cone be devided by the plane?
Asked by nihalpinki123 | 06 Oct, 2019, 09:55: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
If triangle abc and triangle dbc are on the same base bc with ab=dc and ac=db, then state the one to one correspondence between the vertices. Pls ans this question
Asked by chaudhurisrijani | 08 Sep, 2019, 01:12: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
If the areas of two similar triangles, ∆PQR and ∆XYZ are 162sq.cm and 200sq.cm respectively. Find the ratio of their perimeters.
question image
Asked by rizwan2959 | 21 Oct, 2018, 12:49: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Please solve this question 
question image
Asked by vikasg13.hardware | 30 Jun, 2018, 12:01: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Given two triangles ABC and DEF with , .Are the two triangles similar ? If yes, by which rule? Explain
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
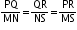Given two triangles PQR and MNS with .  Are the two triangles RPQ and MNS similar ? If yes, by which rule? Explain your Answer..
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×