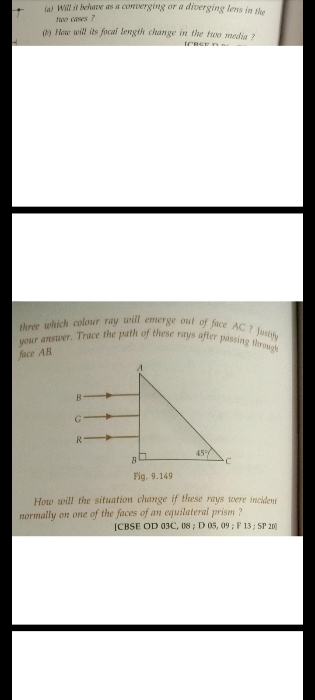
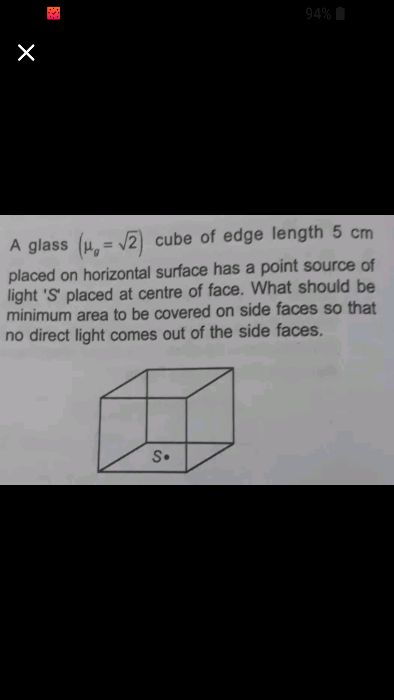
CBSE Class 12-science Answered

Figure (a)

Figure (b)

Figure (c)

The above figure shows the image formation by a convex lens.

Assumptions made in the derivation:

• The lens is thin so that distances measured from the poles of its surfaces can be taken as equal to the distances from the optical centre of the lens.

• The aperture of the lens is small.

• The object consists only of a point lying on the principle axis of the lens.

• The incident ray and refracted ray make small angles with the principle axis of the lens.

A convex lens is made up of two convex spherical refracting surfaces.

The first refracting surface forms image I of the object O [figure (b)].

Image I₁ acts as virtual object for the second surface that forms the image at I [figure (c)]. Applying the equation for spherical refracting surface to the first interface ABC, we obtain

A similar procedure applied to the second interface ADC gives

For a thin lens, BI₁ = DI₁

Adding equations (i) and (ii), we obtain

Suppose the object is at infinity i.e.,

OB ? ? and DI ? f

Equation (iii) gives

The point where image of an object placed at infinity is formed is called the focus (F) of the lens and the distance f gives its focal length. A lens has two foci, F and, on either side of it by the sign convention.

BC₁ = R ₁

CD₂ = ?R ₂

Therefore, equation (iv) can be written as

Equation (v) is known as the lens maker’s formula.

From equations (iii) and (iv), we obtain

As B and D both are close to the optical centre of the lens,

BO = ? u, DI = + v, we obtain

Equation (vii) is known as thin lens formula.