How is it that upon doubling the separation between two masses, the force of attraction b/w them is reduced to one fourth??

-Applying the Universal Law of Gravitation, the force of attraction between two masses is given by

-Where, G is the universal gravitational constant, M is the mass of the Earth, m is the mass of any given body and r is the distance between the bodie and the Earth in this case.

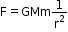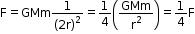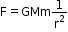-Now its , so if the distance is doubled, r becomes 2r and the equation for F becomes .

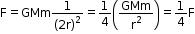-Therefore, on doubling the separation between two masses, the force of attraction b/w them is reduced to one fourth.

 

Hope this helped :)