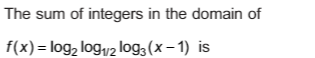CBSE Class 11-science Answered

Domain is the set of all values of a function that 'x' can take.

Range is the set of all values of a function that 'y' can take.

(1) Fractional function

Consider the function

In this function x can take all the values except zero.

Therefore,

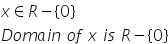
Now let us consider the range of f(x).

Again f(x) can take all the values except 0.

Therefore,

(2) Polynomial function

Domain of a polynomial function is the set of real numbers

And the range of polynomial function is also the set of real numbers.

In the above example, domain is the set of Real Numbers.

Range is the set of positive real numbers, including zero.

(3) Greatest integer function

Domain of greatest integer function is the set of real numbers.

Range of greatest integer function is the set of integers.

The graph of the greatest integer function is as follows: