CBSE Class 11-science Answered

The angular diameter of a flat circular object (disc) can be calculated using the formula:

in which  is the angular diameter, and  and 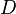 are the visual diameter of and the distance to the object, expressed in the same units. When  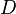is much larger than ,  may be approximated by the formula , in which case the result is in radians.

For a round spherical object whose actual diameter equals , the angular diameter can be found with the formula:

The difference is due to when you look at a sphere, the edges are the tangent points, which are somewhat on your side of the facing hemisphere cross section.  measures opposite/adjacent, whereas  measures opposite/hypotenuse. For practical use, the distinction between the visual diameter  and the actual diameter  only makes a difference for spherical objects that are relatively close.

For very distant or stellar objects, the Small-angle approximation can also be used:

Which simplifies the above equations to:

 (for small )