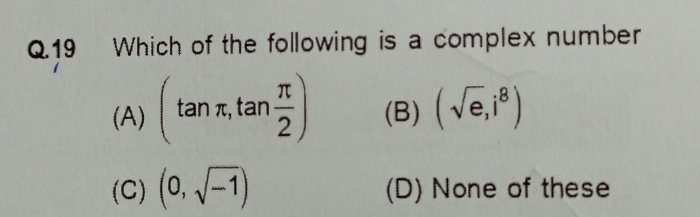Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

how can we find the number of positive integers n for which n^2+96 is a perfect square?
Asked by | 26 Aug, 2012, 06:39: PM
answered-by-expert Expert Answer

Suppose that n2 + 96 = m2 for some positive integer m, then

m2 - n2 = 96
(m - n)(m + n) = 96 = 25 × 3

96 has 12 divisors which come in pairs and since m - n < m + n they are

m - nm + n
1 96
2 48
3 32
4 24
6 16
8 12

For each of the 6 cases solve for m and n and verify which pairs, if any, satisfy your requirements.

Answered by | 26 Aug, 2012, 06:50: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Maths
find square root of 7+24i
Asked by tahikpreet0001 | 17 Apr, 2024, 06:41: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
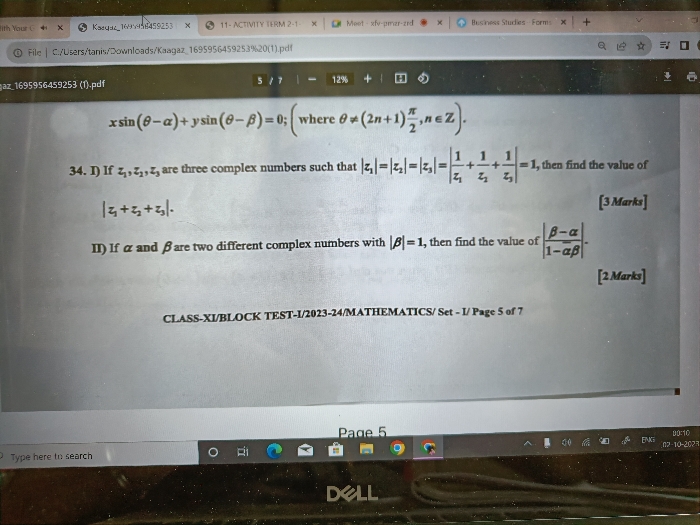
CBSE 11-science - Maths
if α, ß, Γ be the roots of the equation x^3+px^2+qx+r=0 then find the value of (α+ß-3Γ)(ß+Γ-3α)(α+Γ-3ß)
Asked by nitinkrjsr07082008 | 15 Apr, 2024, 11:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
show me the process to solve the problem
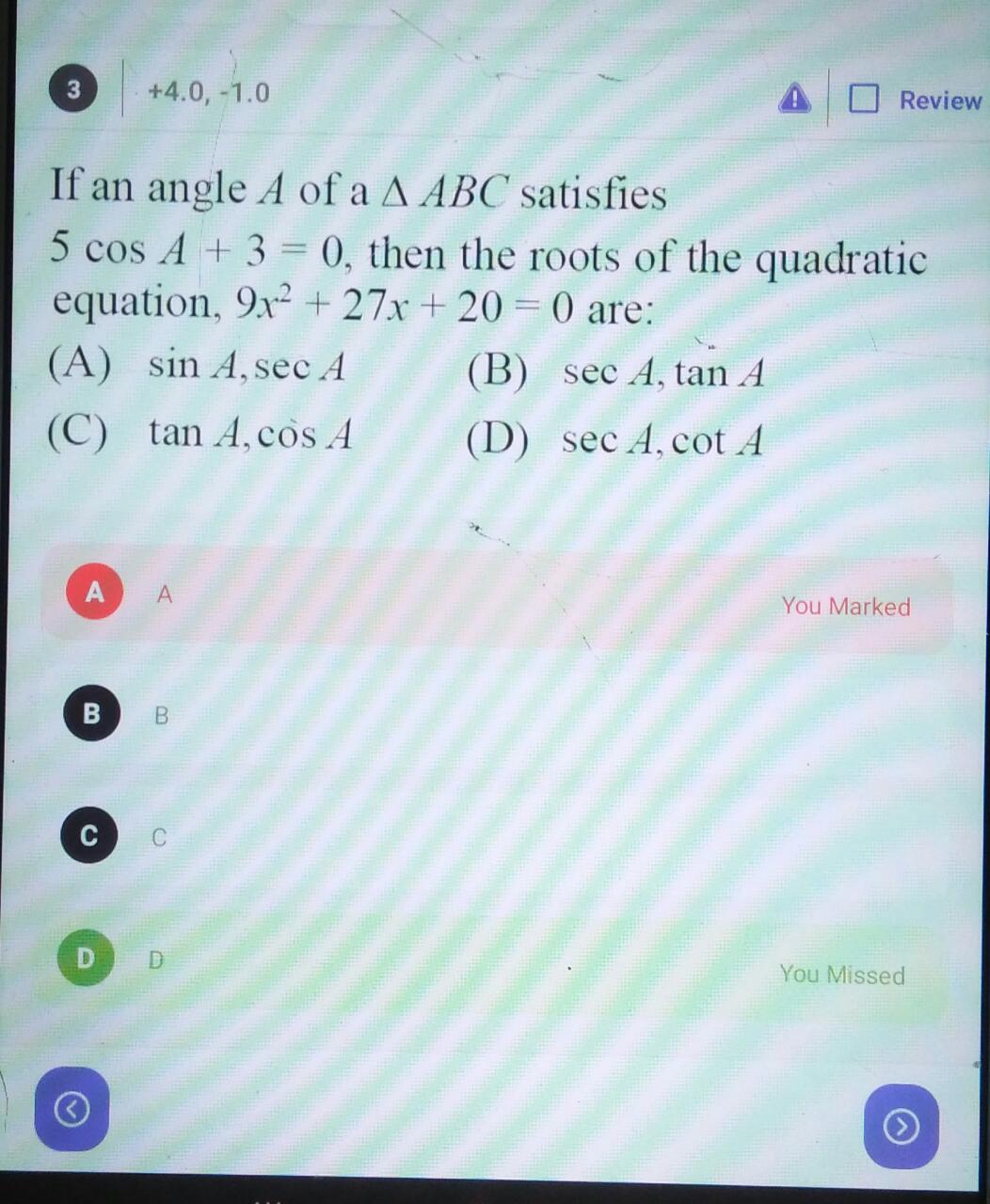
question image
Asked by khairulmasud380 | 08 Feb, 2024, 12:22: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
express in the form of a+ib (i)(1-i)^4
Asked by moulya123 | 08 Jan, 2024, 06:18: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
question number 34
question image
Asked by saanvichawla2007 | 02 Oct, 2023, 12:10: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
For a real number r, the quadratics x² + (r - 1) x + 6 and x² + (2r + 1) x + 22 have a common real root. The sum of the possible values of r can be expressed as a/ b where a, b are relatively prime positive integers. Compute 10a + b
Asked by Bhaveshkr211 | 30 Jul, 2023, 05:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Pls solve
question image
Asked by sdmbotch1123 | 18 Jan, 2023, 11:01: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
solve
question image
Asked by Imotheph1504 | 19 Dec, 2022, 08:19: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
the roots of -18i
Asked by simrangurdasani05 | 17 Jul, 2022, 03:39: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
complete solution set of the equation |x^2-3|+|2-x|=|x^2-x-1|
Asked by rajshekhara348 | 20 Jun, 2022, 11:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×