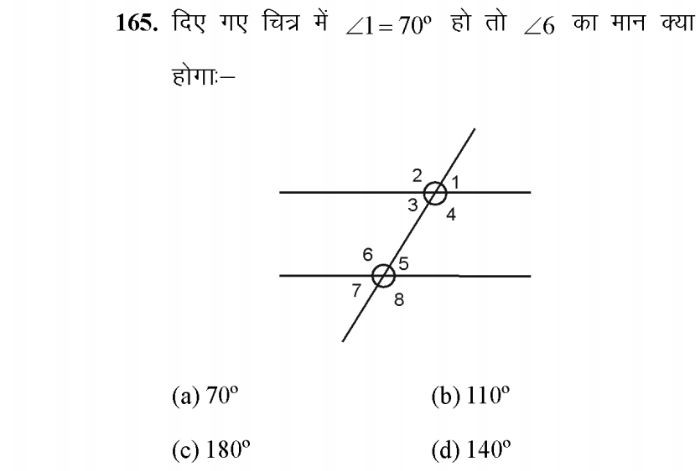
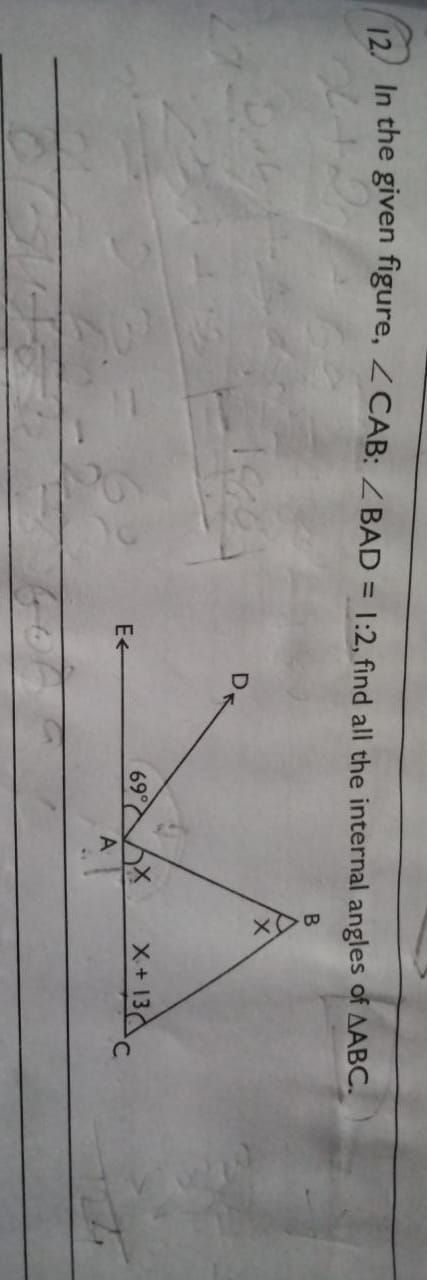
CBSE Class 9 Answered

Early study of triangles can be traced to the 2nd millennium BC, in Egyptian mathematics (Rhind Mathematical Papyrus) and Babylonian mathematics. Systematic study of trigonometric functions began in Hellenistic mathematics, reaching India as part of Hellenistic astronomy. In Indian astronomy, the study of trigonometric functions flowered in the Gupta period, especially due to Aryabhata (6th century). During the Middle Ages, the study of trigonometry continued in Islamic mathematics, whence it was adopted as a separate subject in the Latin West beginning in the Renaissance with Regiomontanus. The development of modern trigonometry shifted during the western Age of Enlightenment, beginning with 17th-century mathematics (Isaac Newton and James Stirling) and reaching its modern form with Leonhard Euler.

The term "trigonometry" derives from the Greek "?????????????" ("trigonometria"), meaning "triangle measuring", from "???????" (triangle) + "???????" (to measure).

Our modern word "sine", is derived from the Latin word sinus, which means "bay", "bosom" or "fold", translating Arabic jayb. The Arabic term is in origin a corruption of Sanskritj?v? "chord". Sanskrit j?v? in learned usage was a synonym of jy? "chord", originally the term for "bow-string". Sanskrit j?v? was loaned into Arabic as jiba.

Ancient Greek and Hellenistic mathematicians made use of the chord. Given a circle and an arc on the circle, the chord is the line that subtends the arc. A chord's perpendicular bisector passes through the center of the circle and bisects the angle. One half of the bisected chord is the sine of the bisected angle, that is,

 chord(theta) = 2sin(theta/2)

The first trigonometric table was apparently compiled by Hipparchus of Nicaea (180 – 125 BCE), who is now consequently known as "the father of trigonometry." Hipparchus was the first to tabulate the corresponding values of arc and chord for a series of angles.

The next significant developments of trigonometry were in India. Influential works from the 4th–5th century, known as the Siddhantas (of which there were five, the most complete survivor of which is the Surya Siddhanta) first defined the sine as the modern relationship between half an angle and half a chord, while also defining the cosine,versine, and inverse sine. Soon afterwards, another Indian mathematician and astronomer, Aryabhata (476–550 AD), collected and expanded upon the developments of the Siddhantas in an important work called the Aryabhatiya. The Siddhantas and the Aryabhatiya contain the earliest surviving tables of sine values and versine(1 ? cosine) values, in 3.75° intervals from 0° to 90°, to an accuracy of 4 decimal places. They used the words jya for sine, kojya for cosine, utkrama-jya for versine, andotkram jya for inverse sine. The words jya and kojya eventually became sine and cosine respectively after a mistranslation described above.

In the 7th century, Bhaskara I produced a formula for calculating the sine of an acute angle without the use of a table. He also gave the following approximation formula for sin(x), which had a relative error of less than 1.9%.

sinx~ 16x(pi-x)/[5pi² - 4x (pi-x)] (0<x<pi/2)