Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 9 Answered

From a given point in the interior of an equilateral triangle,perpendiculars are drawn on the three sides.the lengths of the perpendicularare 14cm,10cm & 6cm. Find the area of triangle.
Asked by araima2001 | 14 Sep, 2014, 05:02: PM
answered-by-expert Expert Answer

∆ABC is an equilateral triangle.

Let ABC be equilateral triangle of side 'a' cm.
 
Let P be a point in the interior of the ∆ABC. so PQ⊥BC, PR⊥CA and PS⊥AB
 
So PS = 14 cm, PQ = 10 cm and PR = 6 cm
 
Area of ∆ABC = Area of ∆APB + Area of ∆BPC + Area of ∆CPA
 
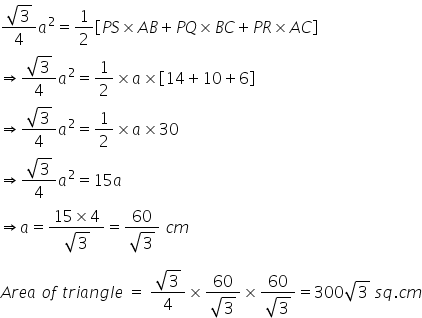
fraction numerator square root of 3 over denominator 4 end fraction a squared equals 1 half open square brackets P S cross times A B plus P Q cross times B C plus P R cross times A C close square brackets rightwards double arrow fraction numerator square root of 3 over denominator 4 end fraction a squared equals 1 half cross times a cross times open square brackets 14 plus 10 plus 6 close square brackets rightwards double arrow fraction numerator square root of 3 over denominator 4 end fraction a squared equals 1 half cross times a cross times 30 rightwards double arrow fraction numerator square root of 3 over denominator 4 end fraction a squared equals 15 a rightwards double arrow a equals fraction numerator 15 cross times 4 over denominator square root of 3 end fraction equals fraction numerator 60 over denominator square root of 3 end fraction space c m A r e a space o f space t r i a n g l e space equals space fraction numerator square root of 3 over denominator 4 end fraction cross times fraction numerator 60 over denominator square root of 3 end fraction cross times fraction numerator 60 over denominator square root of 3 end fraction equals 300 square root of 3 space s q. c m
Answered by Dharma Teja | 14 Sep, 2014, 11:25: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 9 - Maths
find the area of triangle whose sides are 40cm,24 cm,32cm?
Asked by seemarajpoot01101986 | 29 Nov, 2023, 04:40: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
find the area of a triangle two sides of which are 18cm and 10cm and it's perimeter is 42cm
Asked by shrikantsalunkhe1012 | 10 Jun, 2023, 06:47: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Area of an isosceles right angled triangle is 50cm ² find the length of equal side
Asked by vasumathir1978 | 25 Aug, 2021, 11:08: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
the perimeter of a triangular field is 280 dm. If two of its sides are 78 dm and 50 dm,find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
Asked by saanvichhikara07 | 23 Sep, 2020, 08:10: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
there is a slide in a park. One of its side walls has been painted in some colour with a message "keep the park clean and green if the sides of the wall are 1511 and 6 cm find the area painted in colour
Asked by kynarahman | 20 Aug, 2020, 07:53: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Two sides of a triangle are 8cm and 11cm and it's perimeter is 32cm.The third side is : a)4cm b)13cm c)14cm d)16cm
Asked by arumugaperumalr17 | 09 Aug, 2020, 10:00: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
a parallelogram has two sides 16cm and 25 cm and the diagonal is 65m long .find the area of the parallelogram
Asked by gauravbhardwaj65950 | 25 Apr, 2020, 09:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Aapka it in the shape of a square with diagonal 32 cm and an isosceles triangle of days. It's and and side 6 cm each has to be made of three different Shades as known as shown in the figure 12.17 how much paper of a ship has been used in
Asked by kirtisatpute995 | 14 Feb, 2020, 11:22: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
A kite in the shape of a square with a diagonal 32 cm and Isis kilis triangle of base 8 cm and side 6 cm each is to be made of three different Shades as shown in the figure 12.17 how much paper of each shade has been used in it. Has been used in it.
question image
Asked by kirtisatpute995 | 14 Feb, 2020, 11:21: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
A triangle has sides 35 cm 54 cm and 61 cm long find its area also find the smallest of it's altitude altitude altitude
Asked by karanbora625 | 29 Oct, 2019, 12:16: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×