CBSE Class 9 Answered
Expert Answer
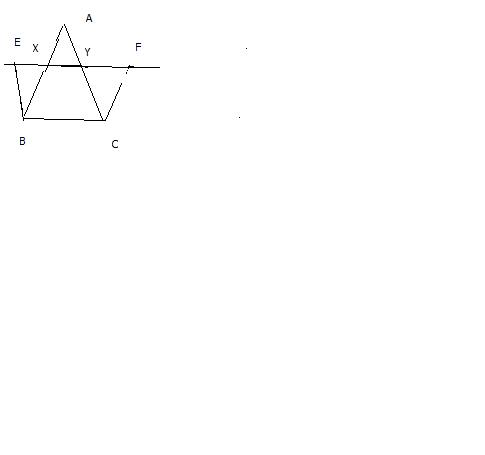
Given : XY is a line parallel to side BC of a triangle ABC. If BE II AC and CF II AB meet XY at E and F respectively
To Prove :
ar(ABE) = ar(ACF)
Proof:
XY // BC (Given )
EB // AC i.e EB // YC.
Quad EBCY is a parallelogram
Similarly FCBXis a parallelogram.
They are on the same base BC and between the same parallels BC and EF.
Therefore AR(//gm EBCY) = Ar (//gm FCBX)
Subtracting Area(Trap XYCB) from both sides , we get
Ar (triangle EBX) = Ar (triangle CFY)
Adding Ar (trangle AXY) to both sides , we have
ar(ABE) = ar(ACF)
Application Videos
-
Application based problem on Quadrilateral ...
This video explains one of the applications of Quadrilateral with the help ... -
Area of a Parallelogram given its base and height
This video explains a case study question which make use of the formula ...
-
Triangle and parallelogram lying on the same base and b ...
This video explains a case study question where a triangle and a paralle...
-
Triangle and parallelogram lying on the same base and b ...
This video explains a case study question where a triangle and a paralle...
-
Triangle and parallelogram lying on the same base and b ...
This video explains a case study question where a triangle and a paralle...
Concept Videos
-
Concept of Area of Region
Concept of area of Geometrical figures. Geometrical figures on the same ba... -
Area related to Parallelograms
This video explains the relation between the area of two parallelograms,...
-
Area of Triangles
This video explains that the areas of the triangles drawn on the same base ... -
Concept of area of Geometrical figures
Concept of area of Geometrical figures. Geometrical figures on the same bas... -
Relation between area of two parallelogram
Relation between the area of two parallelograms, a triangle and a parallelo...
ANSWERED BY EXPERT ANSWERED BY EXPERT ANSWERED BY EXPERT ANSWERED BY EXPERT ANSWERED BY EXPERT ANSWERED BY EXPERT ANSWERED BY EXPERT ANSWERED BY EXPERT ANSWERED BY EXPERT ANSWERED BY EXPERT
