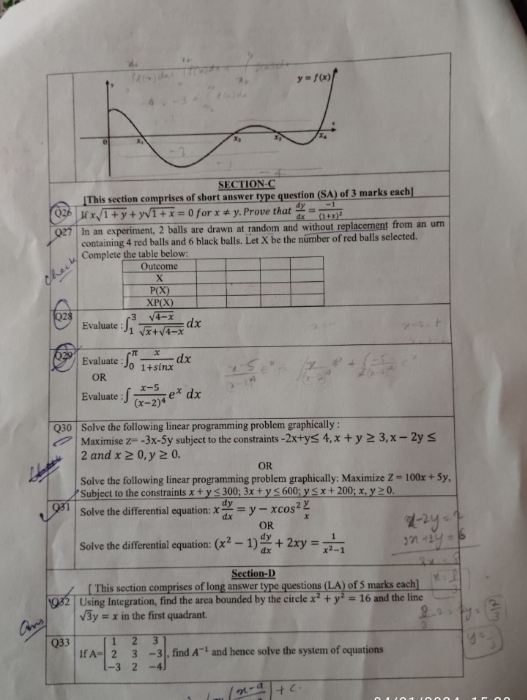
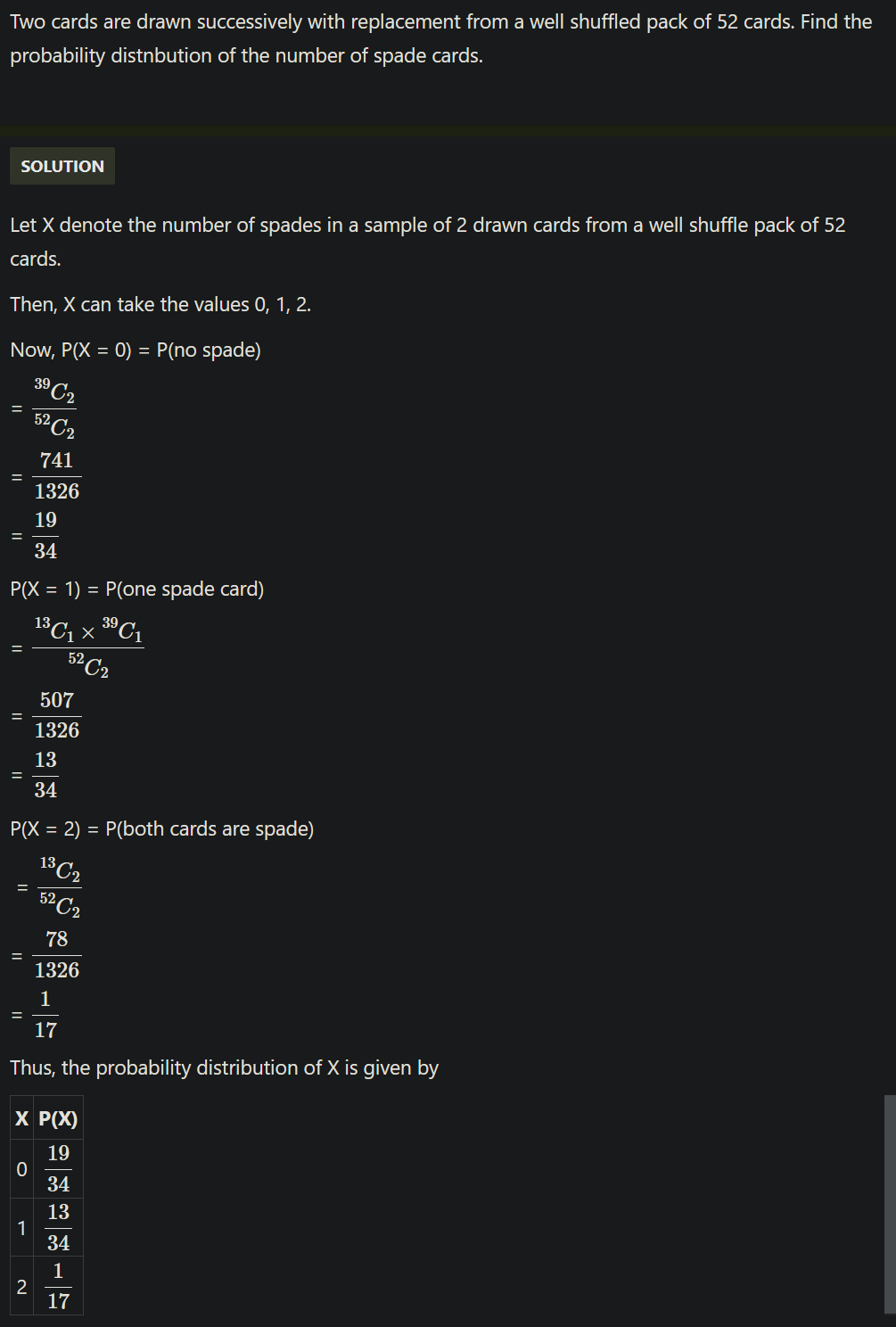
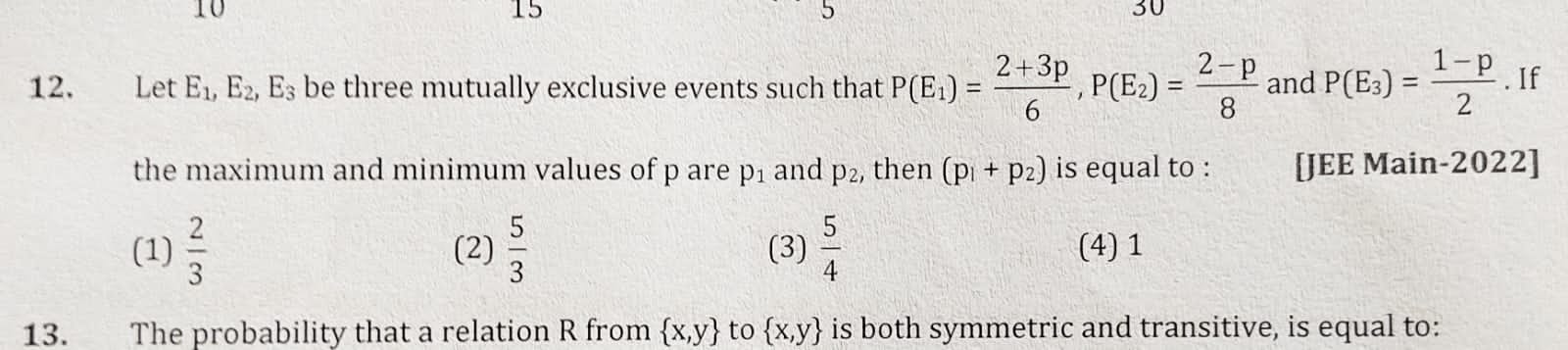CBSE Class 12-science Answered
Find the probability distribution of the number of sixes in a simultaneous toss of three dice.
Asked by Aarthi Vishwanathan | 23 Dec, 2013, 06:50: PM
Expert Answer
A six can be obtained in one of the dice, two of the dices or all 3 of the dices.
Let P(X) represent the probavility of getting x sixes in a throw of 3 dice.
Probability of getting 1 six. That is, P(1) :
Probability of obtaining a six in one dice is 1/6.
Since a six can be obtained in the first, second or the third dice, probability of
getting 1 six in a throw of 3 dices is : 1/6 + 1/6 + 1/6 = 3/6 = 1/2.
Probability of getting 2 sixes. That is, P(2) :
Probability of obtaining sixes in 2 dice is (1/6) X (1/6).
2 dices can be chosen from 3 dices in 3C2 = 3 ways.
Thus, the probability of getting 2 sixes in a throw of 3 dices is :
3 X (1/6) X (1/6) = 3/36 = 1/12.
Probability of getting 3 sixes. That is, P(3) :
Probability of obtaining sixes in all 3 dice is (1/6) X (1/6) X(1/6).
There is only one way in which 3 dice can be chosen from 3 dice.
Thus, the probability of getting 3 sixes in a throw of 3 dices is :
(1/6) X (1/6) X (1/6) = 1/216.
Thus, the probability distribution is :
X 1 2 3
P(X) 1/2 1/12 1/216
Answered by Vimala Ramamurthy | 24 Dec, 2013, 08:41: AM
Concept Videos
-
Conditional Probability
This video explains the concept of conditional probability and solves probl... -
Concepts on Partition of a sample space
Partition of a sample space, law of total probability. Bayes' Theorem. -
Concepts on Binomial Distribution
This video introduces and explains Binomial Distribution. -
Concepts on distribution of random variables
This video deals with the concepts of random variables. -
Mean and Variance of Random Variables ...
The video covers topics such as finding the mean of random probability dist...
CBSE 12-science - Maths
Asked by annapoornaa429 | 31 Mar, 2024, 08:23: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by janusingh736 | 13 Mar, 2024, 04:19: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by khushisjkvm | 04 Jan, 2024, 07:14: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by ashwinskrishna2006 | 26 Dec, 2023, 07:34: PM
ANSWERED BY EXPERT
CBSE 12-science - Maths
Asked by babitdevi283 | 14 Nov, 2023, 09:42: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by surajsharmaisonline | 20 Jan, 2023, 12:28: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by arjunsah797 | 03 May, 2022, 10:04: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by rairp2017 | 27 May, 2021, 12:21: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by 1999shaileshraj | 22 Feb, 2020, 11:50: AM
ANSWERED BY EXPERT
