CBSE Class 12-science Answered
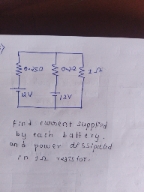
Find the current in each resistor
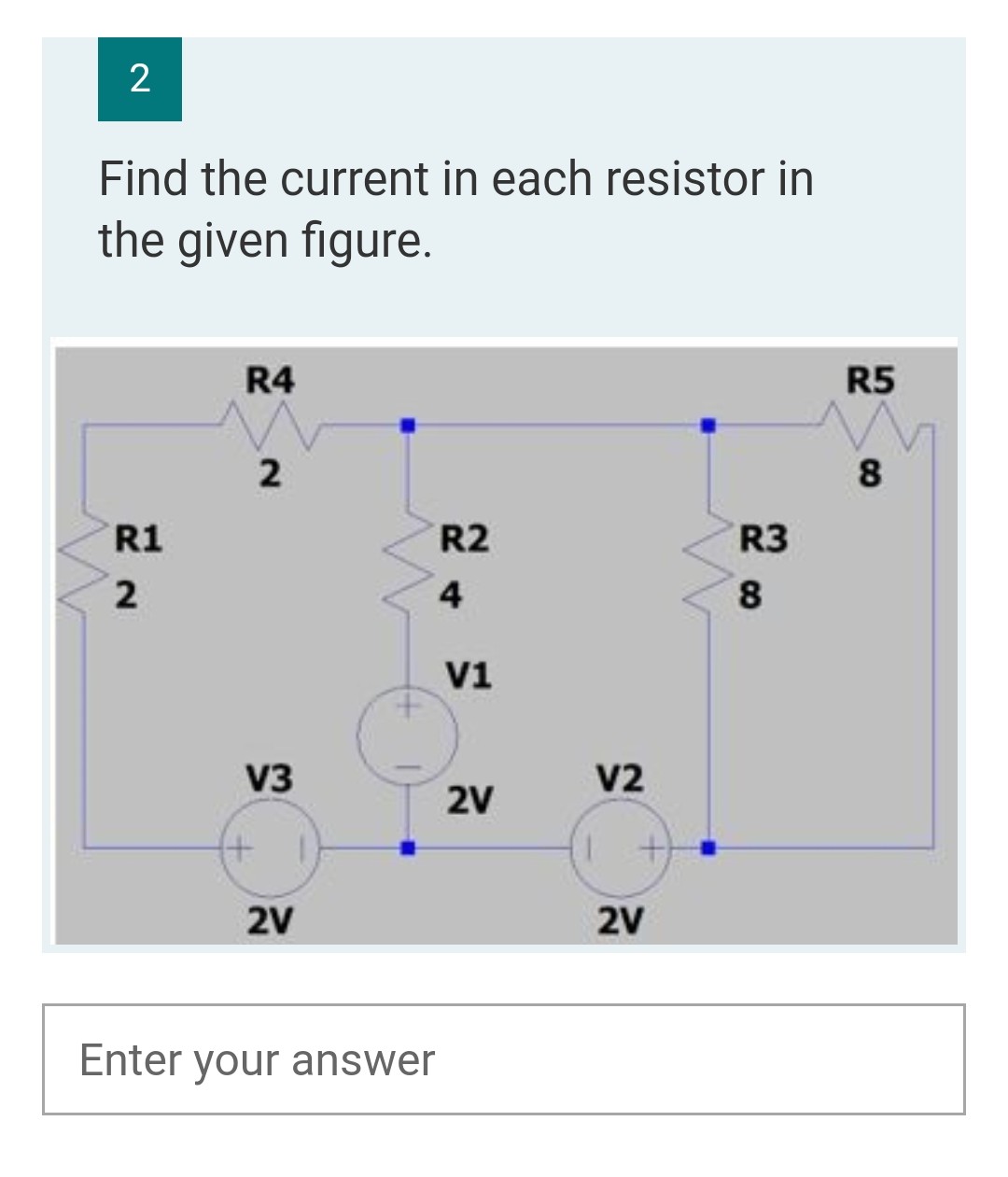
Asked by najeeb.razvi | 09 Aug, 2021, 06:45: PM
Expert Answer
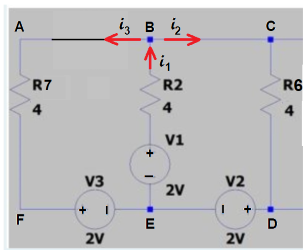
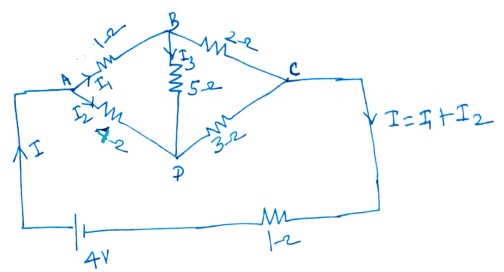
In the given circuit R1 and R4 are in series .
Hence Equivalent resistance R7 = 4Ω replaces resistors R1 and R4 in the circuit shown above.
Similarly , in the given circuit, R3 and R5 are in parallel.
Hence Equivalent resistance R6 = 4Ω replaces resistors R3 and R5 in the circuit shown above.
Let us assume the current distribution as shown in figure.
If we apply Kirchoff's voltage law to the loop ABEFA , we get
4 
1 + 4 3 + 2 = 2 or 1 = - 3 ............................ (1)
1 + 4 3 + 2 = 2 or 1 = - 3 ............................ (1)If we apply Kirchoff's voltage law to the loop BCDEB , we get
4 1 + 4 2 + 2 = 2 or 1 = - 2 ...........................(2)
1 + 4 2 + 2 = 2 or 1 = - 2 ...........................(2) At node B , if we apply Kirchoff's current law , we get 1 = 2 + 3 ...............................(3)
1 = 2 + 3 ...............................(3)From equations (1), (2) and (3) , we get , 1 = 2 = 3 = 0
1 = 2 = 3 = 0Hence current through all resistors is zero
Answered by Thiyagarajan K | 09 Aug, 2021, 08:33: PM
CBSE 12-science - Physics
Asked by komalbrar0987 | 17 May, 2023, 06:15: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by nudratnigar | 10 May, 2022, 12:02: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by divyabharti14042004 | 18 Jan, 2022, 02:52: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by carthi66 | 11 Nov, 2021, 02:49: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by umeshts142 | 13 Oct, 2021, 08:14: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by najeeb.razvi | 09 Aug, 2021, 06:45: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by hitanshu92 | 09 Jul, 2021, 10:22: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by niveshpritmani | 02 Aug, 2020, 11:50: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by sakshisharma23498 | 12 Jul, 2020, 09:55: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by pranavhv99 | 12 Dec, 2019, 10:57: AM
ANSWERED BY EXPERT