CBSE Class 11-science Answered
Find the coefficient of 1/x in the expansion of (1+x)^n(1/x+x)^n
I f the sum of binomial coefficients of the expansion (2x+1/x)/^n is equal to 256, then find the term independent of x
Asked by Nirbhay | 05 Nov, 2014, 05:54: AM

Answered by Prasenjit Paul | 07 Nov, 2014, 10:22: AM
Concept Videos
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 30 Sep, 2016, 09:11: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 30 Sep, 2016, 09:15: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM





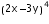 by using binomial expansion.
by using binomial expansion. :
: 