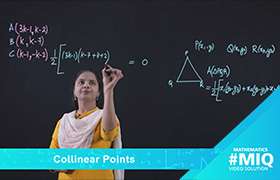CBSE Class 10 Answered
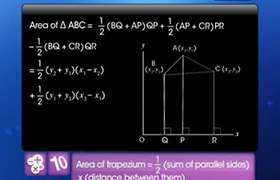
Find the area of the Triangle ABC, with vertex A(1,-4) and midpoint of AB and AC as X(2,-1) and Y(0,-4) respectively.
Asked by nijurajeev7276 | 08 Jan, 2020, 09:52: AM
To find area of the triangle ABC, with vertex A(1,-4) and midpoint of AB and AC as X(2,-1) and Y(0,-4) respectively.
Let B(x,y) and C(a, b)
Midpoint of AB is (2, -1)
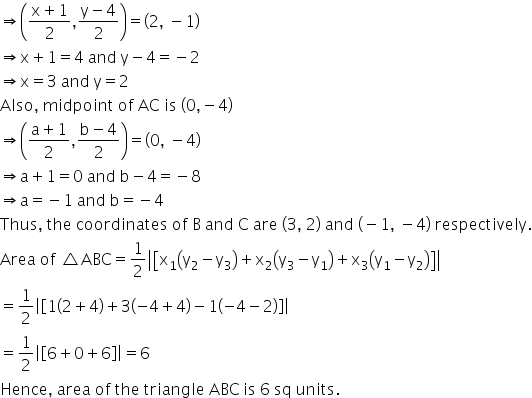
Answered by Renu Varma | 08 Jan, 2020, 10:40: AM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by kadaramyadav | 02 Nov, 2023, 11:02: PM
CBSE 10 - Maths
Asked by priyankakiran2017 | 25 May, 2022, 06:59: AM
CBSE 10 - Maths
Asked by priyankakiran2017 | 25 May, 2022, 06:58: AM
CBSE 10 - Maths
Asked by jaiharekrushna75 | 11 Sep, 2020, 11:56: AM
CBSE 10 - Maths
Asked by dvijaybs45 | 07 Sep, 2020, 08:57: PM
CBSE 10 - Maths
Asked by nijurajeev7276 | 08 Jan, 2020, 09:52: AM
CBSE 10 - Maths
Asked by priyalpathak06 | 05 May, 2019, 11:55: PM