CBSE Class 12-science Answered
Find the angle of intersection of 2 curve x^2y=2 and xy^2=4
Asked by agarwalgolu318 | 13 Aug, 2020, 08:09: PM
The given curves are x2y = 2 ... (i) and xy2 = 4 ... (ii)
From (i), we get y=2/x2
Substituting in (ii), we get x =1
So, we get y = 2
Thus, the point of intesec of the two curves is (1, 2)
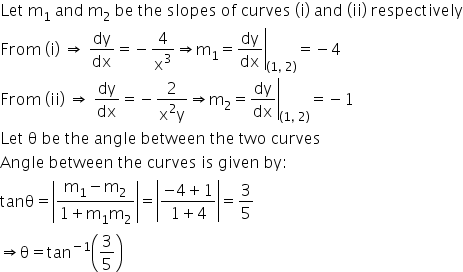
Answered by Renu Varma | 14 Aug, 2020, 11:03: AM
Concept Videos
CBSE 12-science - Maths
Asked by agarwalgolu318 | 13 Aug, 2020, 08:09: PM
CBSE 12-science - Maths
Asked by givduf | 11 Jul, 2020, 09:00: AM
CBSE 12-science - Maths
Asked by sonalchoudhary882 | 22 Oct, 2018, 12:22: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 08:27: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 08:32: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 09:19: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 09:58: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 10:14: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 11 Aug, 2014, 10:06: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 12:43: PM




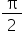 is
is