CBSE Class 10 Answered
find other zeroes of a polynomial 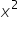 -
-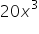 +
+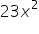 +
+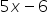 if two of its zeroes are 2 ans 3.
if two of its zeroes are 2 ans 3.
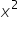 -
-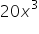 +
+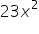 +
+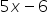 if two of its zeroes are 2 ans 3.
if two of its zeroes are 2 ans 3.
Asked by Akansha | 14 Jun, 2014, 06:33: AM
Please check your question. The question should be as follows:
Find other zeroes of a polynomial x4-20x3+23x2+5x-6 if two of its zeroes are 2 and 3.
Solution: Let the other roots of the polynomial be  and
and  .
.
Sum of the zeroes
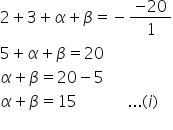
Product of the zeroes:
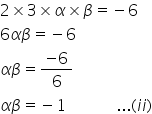
Now,
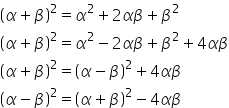
You are given the values of 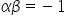 and
and 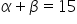
Substitute the given values into the formula.
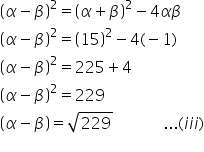
Add equation (i) and (iii).
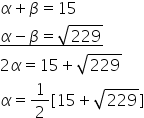
Subtract equation (iii) from (i).
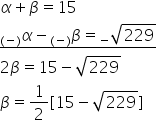
Therefore, the other zeroes of the polynomial are 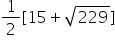 and
and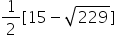 .
.
Answered by Anuja Salunke | 15 Jun, 2014, 08:15: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by anubhutiupadhaya | 14 Mar, 2024, 11:57: AM
CBSE 10 - Maths
Asked by reetudetha | 08 Jan, 2024, 04:12: PM
CBSE 10 - Maths
Asked by mysticsurya201 | 04 Jan, 2024, 08:25: PM
CBSE 10 - Maths
Asked by fatehbahadurtiwari3 | 30 Dec, 2023, 06:25: PM
CBSE 10 - Maths
Asked by dhaneswarnimal80 | 11 Nov, 2023, 06:50: AM
CBSE 10 - Maths
Asked by skandachiranjeevin | 01 Nov, 2023, 08:58: PM
CBSE 10 - Maths
the value 'p'for which polynomials x²-(p²-9)x+8has zeroes equal in magnitude but opposite in sign is


Asked by sazimkhan178 | 16 Sep, 2023, 11:27: AM
CBSE 10 - Maths
Asked by pranavtamboli65 | 09 Jul, 2023, 09:13: PM
CBSE 10 - Maths
Asked by rekhapreetham | 15 Jun, 2023, 08:23: PM
CBSE 10 - Maths
Asked by dimpaldihingia2 | 24 May, 2023, 06:10: PM