CBSE Class 12-science Answered

find area bounded by tangent to 4y=x^2 at (2,1) and lines with equations x=2y and x=3y-3

Asked by jritu1 | 05 Jan, 2016, 01:24: AM

Expert Answer

F o r space t h e space c u r v e space 4 y equals x squared 4 fraction numerator d y over denominator d x end fraction equals 2 x rightwards double arrow fraction numerator d y over denominator d x end fraction equals x over 2 right enclose fraction numerator d y over denominator d x end fraction end enclose subscript a t space left parenthesis 2 comma space 1 right parenthesis end subscript equals 1 H e n c e comma space e q u a t i o n space o f space tan g e n t space a t space left parenthesis 2 comma 1 right parenthesis space i s space y minus 1 equals 1 open parentheses x minus 2 close parentheses rightwards double arrow y equals x minus 1 T h e space b o u n d e d space r e g i o n space i s space s h a d e d space i n space t h e space f i g u r e. left parenthesis 2 comma 1 right parenthesis space i s space a l s o space a space p o i n t space o n space x equals 2 y. space O t h e r space t w o space p o i n t s space o f space i n t e r s e c t i o n s space c a n space b e space f o u n d space b y space s o l v i n g space l i n e a r space e q u a t i o n s space o f space l i n e s space s i m u l tan e o u s l y. W e space g e t space left parenthesis 3 comma space 2 right parenthesis space a n d space left parenthesis 6 comma space 3 right parenthesis space a s space t h e space o t h e r space p o i n t s space o f space i n t e r s e c t i o n. F r o m space x equals 2 space t o space x equals 3 comma space t h e space a r e a space i s space b o u n d e d space b y space y equals x minus 1 space a n d space x equals 2 y. F r o m space x equals 3 space t o space x equals 6 comma space t h e space a r e a space i s space b o u n d e d space b y space x equals 3 y minus 3 space a n d space x equals 2 y. A r e a space b o u n d e d equals space integral subscript 2 superscript 3 open parentheses x minus 1 minus x over 2 close parentheses d x plus integral subscript 3 superscript 6 open parentheses fraction numerator x plus 3 over denominator 3 end fraction minus x over 2 close parentheses d x equals open square brackets x squared over 4 minus x close square brackets subscript 2 superscript 3 plus open square brackets negative x squared over 12 plus x close square brackets subscript 3 superscript 6 equals 5 over 4 minus 1 plus open parentheses negative 27 over 12 close parentheses plus 3 equals 1 space space

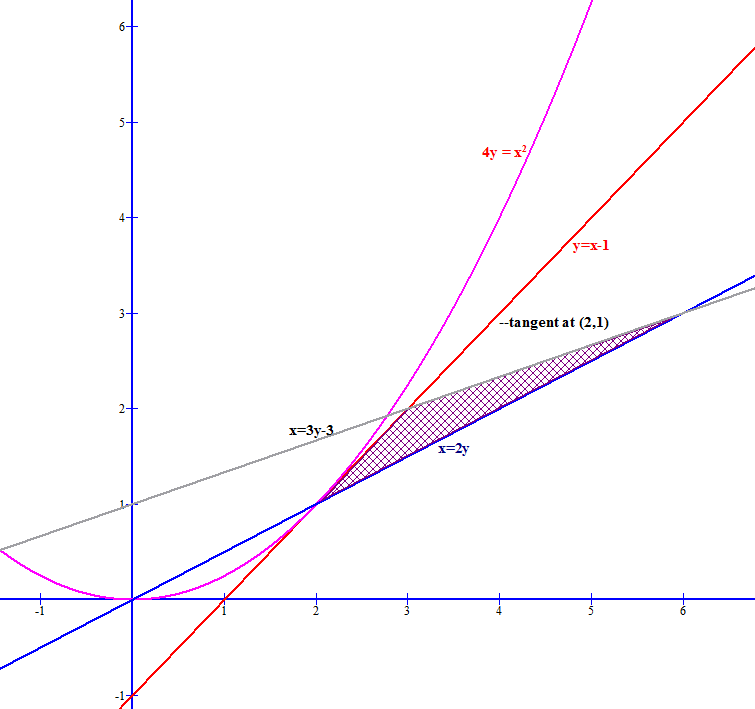
Answered by satyajit samal | 05 Jan, 2016, 11:56: AM

CBSE Class 12-science Answered

Concept Videos

Area Between A Curve and A Line: Introduction

Area Between a curve and a line

Area Between a curve and a line ...

CALL US / WHATSAPP

Please Login or Sign up to continue!

CBSE Class 12-science Answered

Concept Videos

Area Between A Curve and A Line: Introduction

Area Between a curve and a line

Area Between a curve and a line ...

Choose Filters

Open In Ask A Doubt App ?

Get in Touch

Call / Whats App