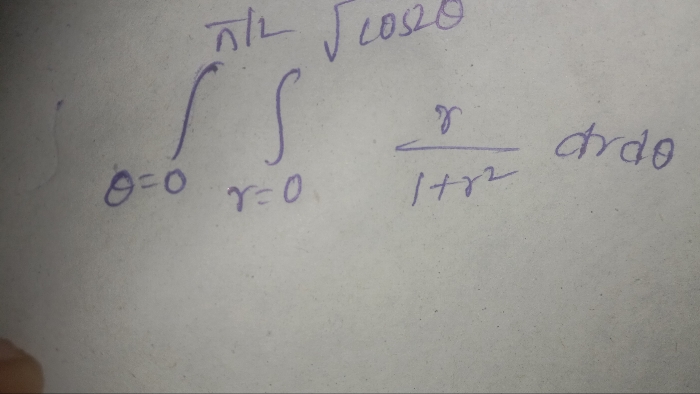CBSE Class 12-science Answered
Evaluate:
?x^2 ?sin?^2 x dx
Asked by Manoj | 16 Mar, 2013, 05:54: AM
write sin^2(x) = [1 - cos(2x)]/2
=1/2?x^2 (1- cos(2x)) dx
=1/2?x^2 dx - 1/2?x^2 cos(2x) dx
=(1/6)x^3 - ?(1/2)x^2 cos(2x) dx
integrate by parts twice
First function= (1/2)x^2 and second function = cos(2x)
?(1/2)x^2 cos(2x) dx = (1/4)x^2 sin(2x) - ?(1/2)x sin(2x) dx
again integrate by parts
first function = (1/2)x, second function = sin(2x)
?(1/2)x^2 cos(2x) dx = (1/4)x^2 sin(2x) + (1/4) x cos(2x) - 1/4? cos(2x) dx
=(1/4)x^2 sin(2x) + (1/4) x cos(2x) - (1/8)sin(2x)+c
so final answer is
(1/6)x^3 - (1/4)x^2 sin(2x) - (1/4) x cos(2x) + (1/8)sin(2x)+c
=1/2?x^2 (1- cos(2x)) dx
=1/2?x^2 dx - 1/2?x^2 cos(2x) dx
=(1/6)x^3 - ?(1/2)x^2 cos(2x) dx
integrate by parts twice
First function= (1/2)x^2 and second function = cos(2x)
?(1/2)x^2 cos(2x) dx = (1/4)x^2 sin(2x) - ?(1/2)x sin(2x) dx
again integrate by parts
first function = (1/2)x, second function = sin(2x)
?(1/2)x^2 cos(2x) dx = (1/4)x^2 sin(2x) + (1/4) x cos(2x) - 1/4? cos(2x) dx
=(1/4)x^2 sin(2x) + (1/4) x cos(2x) - (1/8)sin(2x)+c
so final answer is
(1/6)x^3 - (1/4)x^2 sin(2x) - (1/4) x cos(2x) + (1/8)sin(2x)+c
Answered by | 16 Mar, 2013, 06:14: AM
Concept Videos
CBSE 12-science - Maths
Asked by jprathamesh023 | 23 Mar, 2024, 04:01: PM
CBSE 12-science - Maths
Asked by atulmishra514 | 26 Jan, 2024, 10:15: PM
CBSE 12-science - Maths
Asked by aalavarshitha2005 | 21 Jan, 2024, 05:28: PM
CBSE 12-science - Maths
Asked by atharvaparkar04 | 17 Dec, 2023, 12:59: PM
CBSE 12-science - Maths
Asked by shashinayaka032 | 05 Dec, 2023, 12:46: PM
CBSE 12-science - Maths
Asked by manyarajawat1 | 06 Nov, 2023, 05:03: PM
CBSE 12-science - Maths
Asked by ps9680677 | 26 Oct, 2023, 11:47: AM
CBSE 12-science - Maths
Asked by manasvichandel49 | 19 Oct, 2023, 08:53: AM