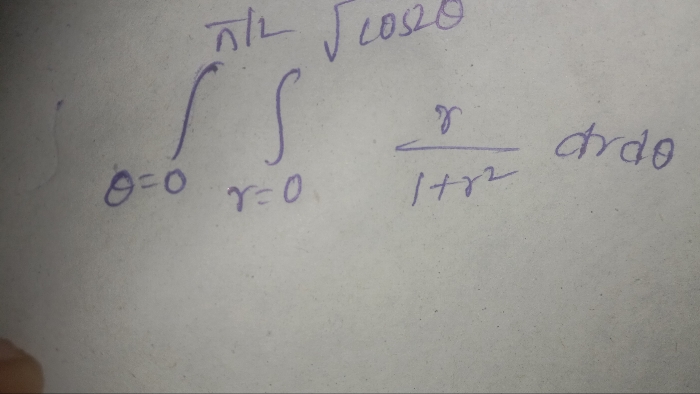CBSE Class 12-science Answered
Evaluate:
∫((x^2+1))/((x^4+1) ) dx
Asked by Manoj | 09 Mar, 2013, 07:32: AM
Expert Answer
I denotes for the value of integral.
(x2+1)/(x4+1)
Divide numerator and denominator by x2, we get:
(1+1/x2)/(1/x2+x2)
(1+1/x2)/[(x-1/x)2 +2] as x2+1/x2 = (x-1/x)2 +2
Let (x-1/x)=t so dt=(1+1/x2 )dx
Therefore, the integral becomes
I = dt/(t2 +2)
1/(2)1/2 tan-1t/(2)1/2 +c
Now, substitute value of t in above to get the answer.
Answered by | 10 Mar, 2013, 03:54: PM
Concept Videos
-
Introduction to Integration ...
This video explains integration as an anti derivative reverse of differenti... -
Integration by substitution
This video explains the use of section formula to find mid point of a line ... -
Integration by partial fractions
This video covers examples related to Integration by partial fractions, whe... -
Integrals using Trigonometic Identities
This video covers examples related to the use of trigonometric identities t... -
Standard formulae for integration of functions
Learn standard formulae for integration of functions involving quadratic fu...
CBSE 12-science - Maths
Asked by jprathamesh023 | 23 Mar, 2024, 04:01: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by atulmishra514 | 26 Jan, 2024, 10:15: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by aalavarshitha2005 | 21 Jan, 2024, 05:28: PM
ANSWERED BY EXPERT
CBSE 12-science - Maths
Asked by atharvaparkar04 | 17 Dec, 2023, 12:59: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by shashinayaka032 | 05 Dec, 2023, 12:46: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by manyarajawat1 | 06 Nov, 2023, 05:03: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by ps9680677 | 26 Oct, 2023, 11:47: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by manasvichandel49 | 19 Oct, 2023, 08:53: AM
ANSWERED BY EXPERT
