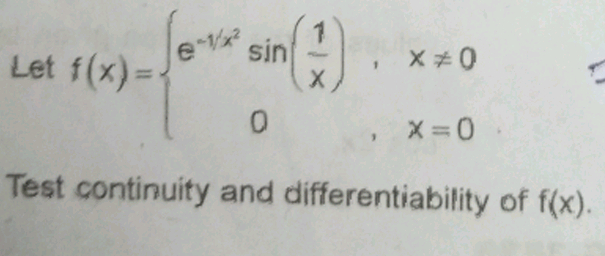CBSE Class 12-science Answered
does there exist a function which is continuous everywhere but not differentiable at exactly 2 points???????????
Asked by Anushri | 25 Jul, 2013, 10:20: PM
Expert Answer
|x| is a function that is continuous everywhere but isn 't differentiable at exactly one point.
Define a function f(x), such that
f(x) = |x| for x<0, f(x) = sinx, for 0?x<22/7, f(x) = |x-22/7| for x?22/7
Then this function is continuous everywhere, but will have two points where it is not differentiable.
Answered by | 25 Jul, 2013, 10:31: PM
Concept Videos
-
Continuous and Discontinuous function
Understand the meaning of function to be continuous and discontinuous, comb... -
Relationship between continuity and differentiability - ...
Relationship between continuity and differentiability, concept of composite... -
Derivative of Parametric Functions
Learn the relation between two variables x and y using the third variable a... -
Second-order derivatives
Learn to find out the second-order derivatives of the given functions. -
Rolle's Theorem and its geometrical interpretation ...
Discuss Rolle's Theorem and its geometrical interpretation. Also discuss La...
CBSE 12-science - Maths
Asked by fehasaf670 | 27 Jan, 2024, 01:39: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by tanyavishwakarma427 | 24 Nov, 2023, 11:56: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by sonkarmukesh007 | 13 Aug, 2023, 08:32: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by unqio66 | 15 May, 2023, 11:48: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by sdmbotch1123 | 21 Dec, 2022, 04:38: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by iasaspirant20s | 09 Oct, 2022, 02:31: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by Raunaksingh4742 | 25 Aug, 2022, 12:31: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by pinkidevnict | 08 Jun, 2022, 07:51: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by suvajyotichaudhury998 | 04 Jun, 2022, 07:54: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by lewisraina069 | 03 Jun, 2022, 06:56: AM
ANSWERED BY EXPERT
