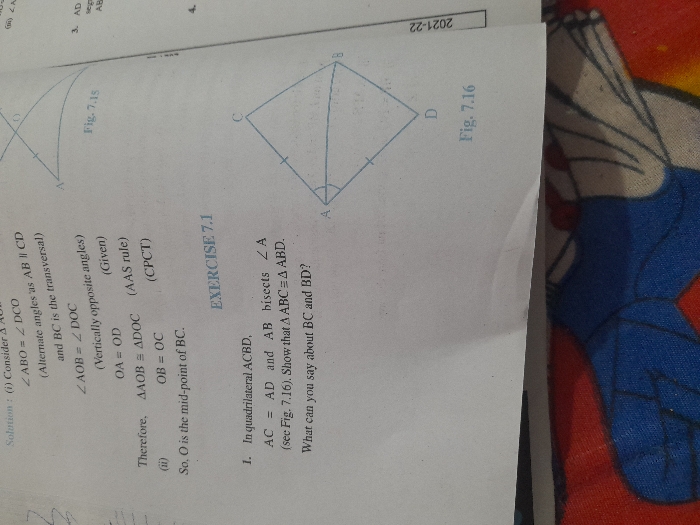
diagonals PR,SQ of an quadrilateral PQRS meet at o provethat PQ+QR+RS+SP>(PR+QS)

In a triangle, sum of two sides is more the third side.

 

So, in triangle PQR;

PQ + QR > PR                                     … (1)

 

In triangle PSR;

PS + SR > PR                                       … (2)

 

Adding (1) and (2);

PQ + QR + RS + SP > 2PR                                … (3)

 

Similarly, it can be proved that

PQ + QR + RS + SP > 2QS               … (4)

 

Adding (3) and (4);

2(PQ + QR + RS + SP) > 2(PR + QS)

i.e. PQ + QR + RS + SP > PR + QS

Hence, proved.