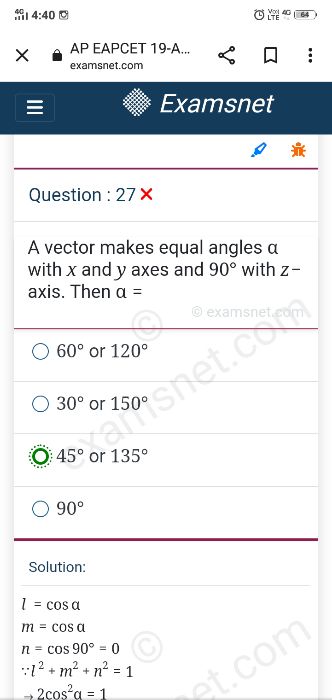
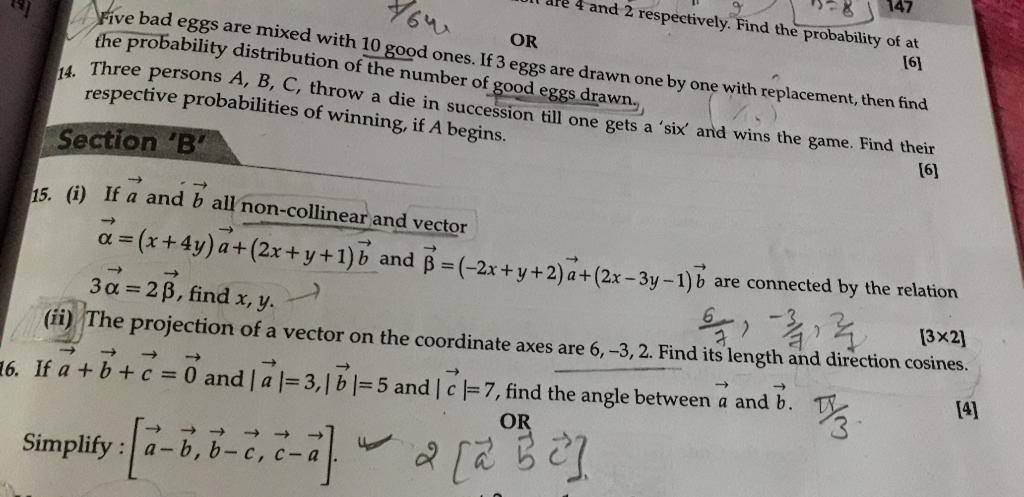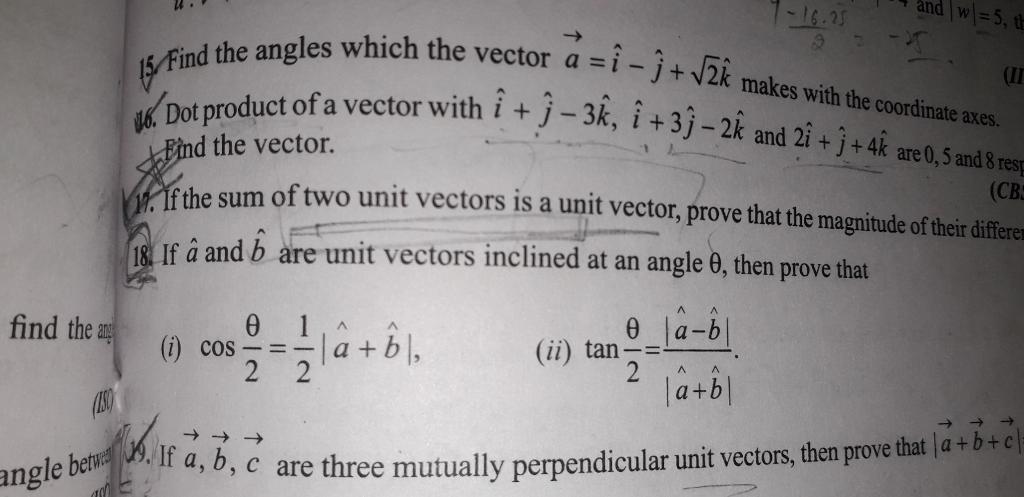CBSE Class 12-science Answered
Determinant Prove
Asked by thebluebloo | 28 May, 2009, 04:59: PM
opening the determinent
a(bc-(b+a)(c-a))-(b-c)(c(c+a)-(a-b)(c-a))+(b+c)((a+c)(b+c)-(a-b)b)
=a(bc-bc+ba-ac+a2)-(b-c)(c2+ca-ac+a2+bc-ba)+(b+c)(ab+ac+bc+c2-ab+b2)
=a(ba-ac+a2)-(b-c)(c2+a2+bc-ab)+(b+c)(ac+bc+c2+b2)
=a2b-a2c+a3-bc2-ba2-b2c+ab2+c3+a2c+bc2-abc+abc+b2c+bc2+b3+ac2+bc2+c3+b2c
=a3+ab2+ac2+ba2+b3+bc2+a2c+b2c+c3
=(a+b+c)(a2+b2+c2))
Answered by | 28 May, 2009, 06:58: PM
Concept Videos
CBSE 12-science - Maths
Asked by sdmbotch1123 | 18 Jan, 2023, 11:01: PM
CBSE 12-science - Maths
If |𝑎⃗| = 3 and −1 ≤ 𝑘 ≤ 2, then |𝑘𝑎⃗| lies in the interval
(a) [0,6] (b) [−3,6] (c) [3,6] (d) [1,2]


Asked by mohdtayyab682 | 18 Jan, 2023, 10:34: PM
CBSE 12-science - Maths
Asked by durgaprasaddurgaprasad174 | 01 Jul, 2022, 05:05: PM
CBSE 12-science - Maths
Asked by sujaychandramouli | 24 May, 2022, 10:46: AM
CBSE 12-science - Maths
Asked by abhimeena1011 | 18 Jan, 2022, 10:43: AM
CBSE 12-science - Maths
Asked by gurupadam3101985 | 11 Apr, 2020, 10:06: AM
CBSE 12-science - Maths
Asked by lovemaan5500 | 07 Feb, 2020, 09:49: AM
CBSE 12-science - Maths
Asked by lovemaan5500 | 07 Feb, 2020, 09:49: AM
CBSE 12-science - Maths
Asked by lovemaan5500 | 16 Dec, 2019, 09:34: PM
CBSE 12-science - Maths
Asked by Vivek.d8765 | 29 Oct, 2019, 10:14: PM