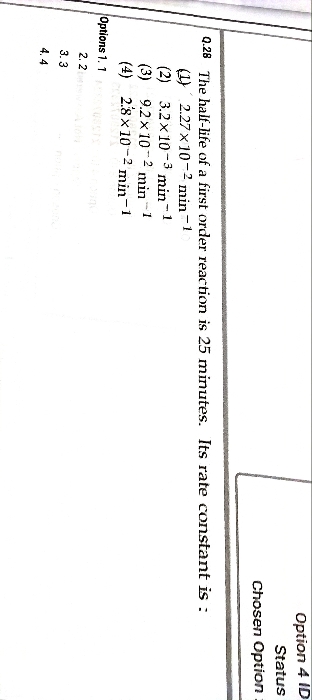
CBSE Class 12-science Answered
Derive lens formula for convex lens.
Asked by polyrelation | 14 Mar, 2019, 09:16: PM
Expert Answer
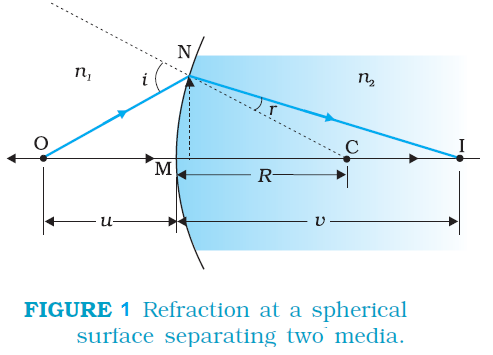
Figure 1 shows the geometry of formation of image I of an object O on the principal axis of a spherical surface with centre of curvature C,
and radius of curvature R. The rays are incident from a medium of refractive index n1, to another of refractive index n2.
As before, we take the aperture (or the lateral size) of the surface to be small compared to other distances involved, so that small
angle approximation can be made. In particular, NM will be taken to be nearly equal to the length of the perpendicular from the point N
angle approximation can be made. In particular, NM will be taken to be nearly equal to the length of the perpendicular from the point N
on the principal axis. We have, for small angles,
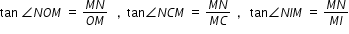
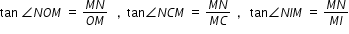
Now for ΔNOC, i is exterior angle. Therefore i = 
NOM + NCM
NOM + NCM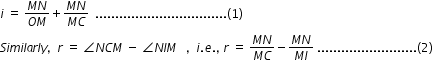
By Snell's law, n1 sin i = n2 sin r or for small angles , n1 i = n2 r ........................(3)
substituting for i and r from (1) and (2), we simplify and rewrite eqn.(3) as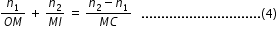 
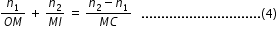
Equation (4) gives us a relation between object and image distance in terms of refractive index of the medium and the radius of
curvature of the curved spherical surface. It holds for any curved spherical surface.
curvature of the curved spherical surface. It holds for any curved spherical surface.
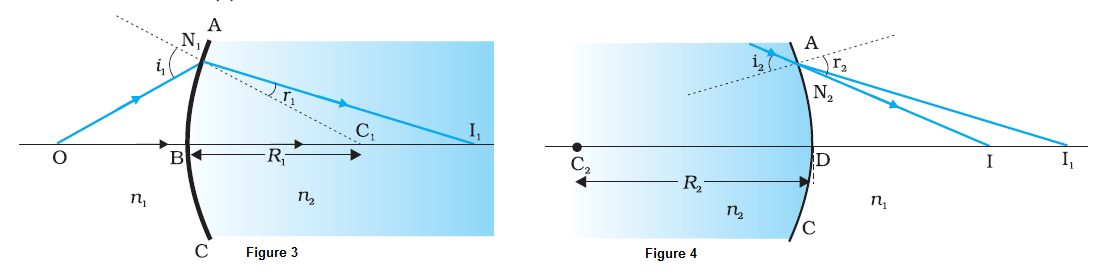
Figure 2 shows the geometry of image formation by a double convex lens. The image formation can be seen in terms of two steps:
(i) The first refracting surface forms the image I1 of the object O [ figure. 3]. The image I1 acts as a virtual object for the second surface
that forms the image at I [ figure 4. ]. Applying Eq. ( 4 ) to the first interface ABC, we get
(i) The first refracting surface forms the image I1 of the object O [ figure. 3]. The image I1 acts as a virtual object for the second surface
that forms the image at I [ figure 4. ]. Applying Eq. ( 4 ) to the first interface ABC, we get
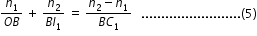
A similar procedure applied to the second interface ADC gives,
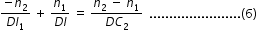
For a thin lens, BI1 = DI1. Adding Eqs. (5) and (6), we get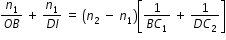 
.............................(6)
Suppose the object is at infinity, i.e., OB → ∞ and DI = f, Eq. (6 ) gives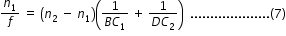
The point where image of an object placed at infinity is formed is called the focus F, of the lens and the distance f gives
its focal length. A lens has two foci, F and F′, on either side of it . By the sign convention, BC1 = + R1, DC2 = –R2
So Eq. (7) can be written as
..........................(8)
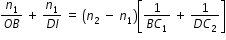.............................(6)Suppose the object is at infinity, i.e., OB → ∞ and DI = f, Eq. (6 ) gives
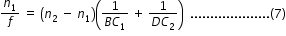
The point where image of an object placed at infinity is formed is called the focus F, of the lens and the distance f gives
its focal length. A lens has two foci, F and F′, on either side of it . By the sign convention, BC1 = + R1, DC2 = –R2
So Eq. (7) can be written as
..........................(8)because n21 = n2 / n1 .Equation (8) is known as the lens maker’s formula. It relates the focal length of given lens to the
radii of curvature of lens and also the refractive index of material of lens. It is useful to design lenses of desired focal length
using surfaces of suitable radii of curvature. Note that the formula is true for a concave lens also. In that case R1is negative,
R2 positive and therefore, f is negative.
From Eqs. (5 ) and (6), we get
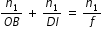...............................(9)Again, in the thin lens approximation, B and D are both close to the optical centre of the lens. Applying the sign convention,
BO = – u, DI = +v, we get
.............................(10)Equation (10) is the familiar thin lens formula. Though we derived it for a real image formed by a convex lens, the formula is valid for both
convex as well as concave lenses and for both real and virtual images.
Answered by Thiyagarajan K | 15 Mar, 2019, 02:15: PM
Concept Videos
-
This video describes the concept of charge, conductors and insulators, and ... -
This video explains the basic properties of electric charges. -
This video describes Coulomb's law to calculate the force between any two p... -
Define electric field in terms of Coulomb's force. Apply superposition prin... -
This video explains the representation of electric field due to a single ch...
CBSE 12-science - Physics
Asked by Abhishek | 23 Mar, 2023, 08:37: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by Jayashri | 06 Mar, 2023, 06:47: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by varma.renu9481 | 06 Mar, 2023, 05:44: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by prachis14 | 06 Mar, 2023, 04:49: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by paresh0311 | 06 Mar, 2023, 04:42: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by anubhutiupadhaya | 06 Mar, 2023, 04:23: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by sagarmishra | 06 Mar, 2023, 04:07: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by bmahalik21 | 05 Mar, 2023, 08:23: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by bmahalik21 | 04 Mar, 2023, 07:03: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by yadavabhishek66686668 | 24 Jan, 2023, 05:32: PM
ANSWERED BY EXPERT