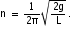CBSE Class 11-science Answered
Derive an expression for the time-period and frequency of oscillation of a cylindrical wooden block floating over water when it is slightly depressed, and released from the state of equilibrium.
Asked by Topperlearning User | 19 May, 2015, 12:03: PM
Consider a cylindrical wooden block of the area of cross-section A, floating up right when immersed to a depth d in a liquid of density 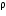 as shown in the figure.
as shown in the figure.
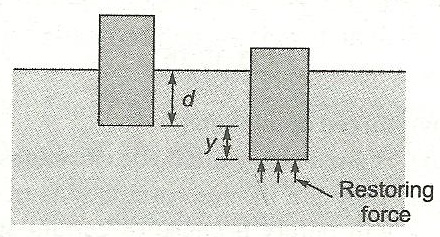
In the equilibrium position, the weight of the block is balanced by the upthrust. From the state of equilibrium, the block is slightly depressed by distance y and released. The mass of the displaced liquid is A y ![]() .
.
It gives rise to an additional upthrust A y ![]() g due to which the resulting motion is simple harmonic. The restoring force = weight of the displaced liquid
g due to which the resulting motion is simple harmonic. The restoring force = weight of the displaced liquid

Answered by | 19 May, 2015, 02:03: PM
Concept Videos
CBSE 11-science - Physics
Asked by Topperlearning User | 19 May, 2015, 10:21: AM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 19 May, 2015, 12:03: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM