CBSE Class 12-science Answered

Hi dear,

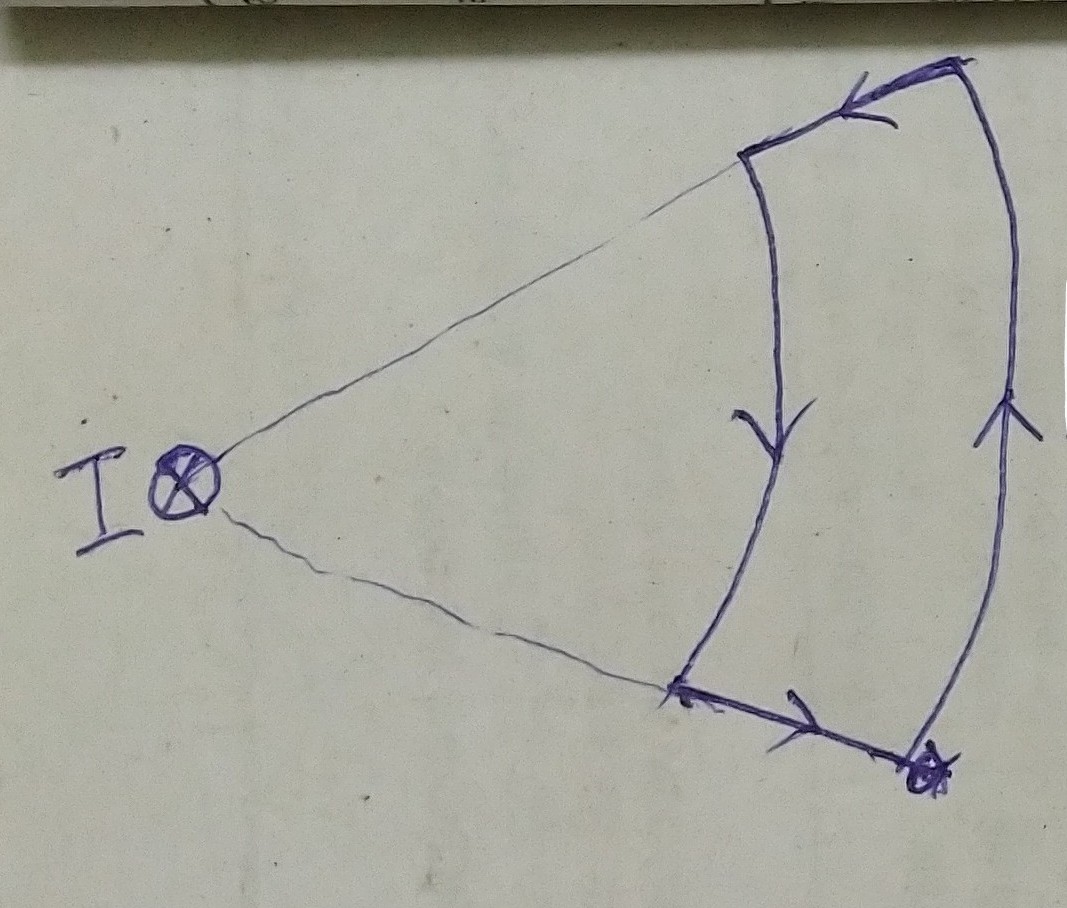
The following figure depicts a circular loop carrying a steady current I. The loop is on y-z plane with the center O at origin and radius R. The x axis is the loop axis. We calculate the magnetic feild at point P on this axis.

Let us take a conducting element dl in the loop. Magnitude dB of the magnetic feild due to dl is

dB = (μ_ο / 4π){ I | dl X r | / r   }

Now r² = x² + R²

Direction of dB is perpendicular to the planr formed by dl and r. The net contributtion along x direction is obtained by integrating dB_x = dB cosθ over the loop.

cosθ = R/ { x² + r²} ^1/2

dBx = μ_ο I dl / 4π { R / { x² + r²}^3/2  }

Summation of elements dl over the loop yeilds 2π R, the circumference of the loop,Thus the magnetic feild at point P due to entire circular loop is 

B = μ_ο I R² / [2 X { x² + r²}3/2 ]

As a special case, the field at the c nenter of the loop . x = 0, hence,

B_o = μ_οI / 2 R

Hope this helped

Regards

Topperlearning.com