CBSE Class 11-science Answered

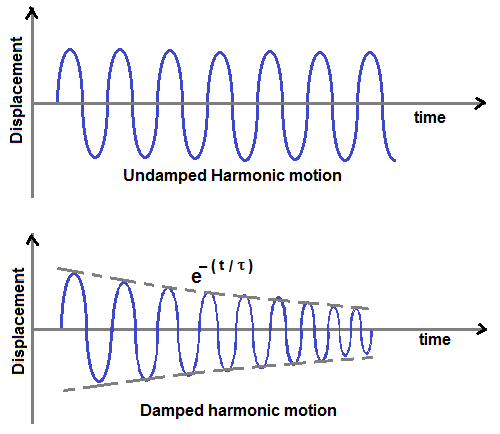
A damped harmonic motion is an oscillatory motion in which the amplitude of oscillation is slowly decreasing

while there is negligible change in period of motion. Loss of amplitude is called damping .

While considering simple harmonic motion, it is assumed that there is no friction force against the motion.

If there is no friction force , an oscillating simple pendulum  or an oscillating mass-spring system will keep on

oscillate indefinitely . But in real situation  , we find amplitude of these oscillations is slowly decreasing .

There are many causes for damping like friction in the oscillating system, air resistance etc.,

For undamped motion , force acting on the oscillating mass is restoring force that is directly proportional to displacement

F = m a(t) = - k x(t)

Where m is mass of oscillating object , a(t) is acceleration that is function of time , k is force constant and

x(t) is displacement that is function of time .

For damped motion there is an additional damping force  that is proportional to velocity is acting on the system.

F = m a(t) =  - k x(t)  - b v(t)

By substituting , a(t) = d²x/dt²  and  v(t) = dx/dt , we write above equation as

 d²x/dt² + ( b / m ) dx/dt  + ( k/m ) x(t) = 0

Solution of displacement to above equation is

where τ = 2m/b is damping time constant and ω' is frequency of damped motion

when damping constant b → 0 ,  displacement and frequecy becomes that of undamped simple harmonic motion.