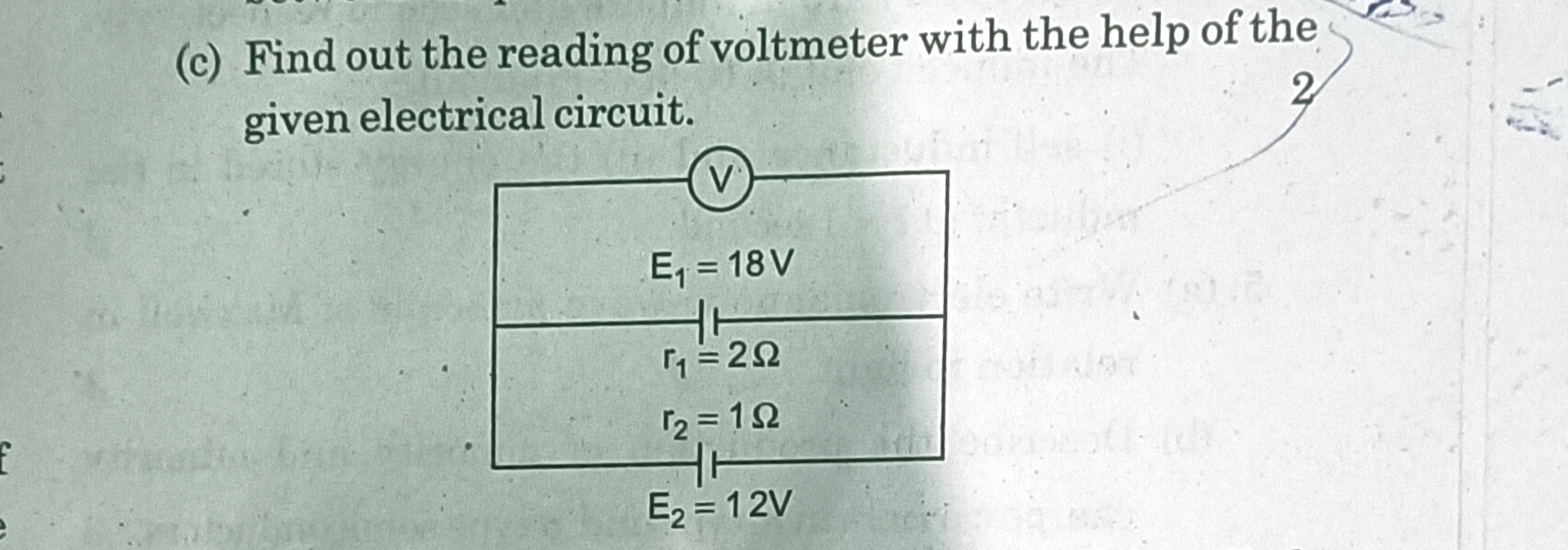
CBSE Class 12-science Answered

power transfer is maximum when r = R which means internal resistance of source equals the load resistance. It is called the maximum power theorem.

Note that we are talking about maximum power and not maximum efficiency. If resistance of the load is greater than the resistance of the source, efficiency is more but overall powr is low.

If internal impedance is made larger than the load the most of the power is dissipated in the source itself, but although the total power dissipated is higher, due to a lower circuit resistance, it turns out that the amount dissipated in the load is reduced.

This can be proved using calculus. I have copied and pasted the proof from wikipedia, url of website is also pasted for further reading.

http://en.wikipedia.org/wiki/Maximum_power_theorem

In the diagram opposite, power is being transferred from the source, with voltage V and fixed source resistance R_S, to a load with resistance R_L, resulting in a current I. By Ohm's law, I is simply the source voltage divided by the total circuit resistance:

The power P_L dissipated in the load is the square of the current multiplied by the resistance:

We could calculate the value of R_L for which this expression is a maximum, but it is easier to calculate the value of R_L for which the denominator

is a minimum. The result will be the same in either case. Differentiating with respect to R_L:

For a maximum or minimum, the first derivative is zero, so

or

In practical resistive circuits, R_S and R_L are both positive. To find out whether this solution is a minimum or a maximum, we must differentiate again:

This is positive for positive values of R_S and R_L, showing that the denominator is a minimum, and the power is therefore a maximum, when

R_S = R_L.