CBSE Class 11-science Answered

Equation

The form of the Schrodinger equation depends on the physical situation.The most general form is the time-dependent Schrödinger equation, which gives a description of a system evolving with time:

Time-dependent Schrödinger equation (general)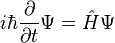

where ? is the wave function of the quantum system, i is the imaginary unit, ? is the reduced Planck constant, and  is the Hamiltonian operator, which characterizes the total energy of any given wave function and takes different forms depending on the situation.

Time-independent equation

The time-dependent Schrodinger equation predicts that wave functions can form standing waves, called stationary states.These states are important in their own right, and moreover if the stationary states are classified and understood, then it becomes easier to solve the time-dependent Schrödinger equation for any state. The time-independent Schrodinger equation is the equation describing stationary states. (It is only used when the Hamiltonian itself is not dependent on time.)

Time-independent Schrodinger equation (general)

In words, the equation states:

When the Hamiltonian operator acts on the wave function ?, the result might be proportional to the same wave function ?. If it is, then ? is a stationary state, and the proportionality constant, E, is the energy of the state ?.