CBSE Class 10 Answered

Steps of construction:

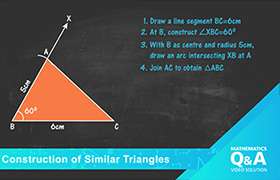
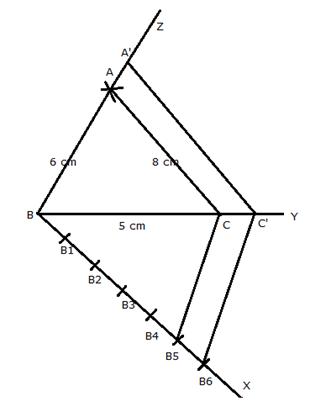
_{1. Draw line segment BC of length 5 cm. With B and C as} centres and radii 6 cm and 8 cm respective draw two arcs intersecting each other at A. Join AB and AC. Now, triangle ABC is the triangle with sides 5 cm, 6 cm and 8 cm.

2. Draw an acute angle XBC on the side opposite to the vertex A.

3. On BX, mark six points B₁, B₂, B₃, B₄, B₅, B₆ and B₇ such that:

BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆

4. Join B₅ to C.

5. From B₆, draw B₆C' parallel to B₅C, intersecting BC produced in C'.

6. From C' draw C'A' parallel to CA, meeting AB produced in A'.

Triangle A'BC' is the required triangle.

OR

Step of Constructions:

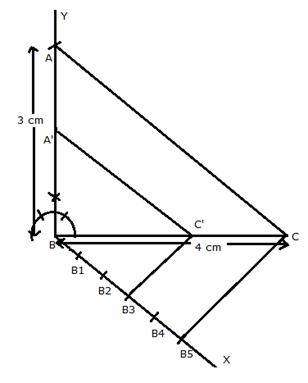
1. Draw BC = 4 cm.

2. At B, draw a ray BY making angle 90^o with BC i.e. YBC = 90^o.

3. From BP, cut BA = 3 cm.

4. Join A and C to get ABC.

5. Through vertex B, draw ray BX making an acute angle with BC on the side opposite to vertex A.

6. On BX cut 5 equal line segments BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅.

7. Join B₅ to C.

8. Through B₃, draw a line parallel to B₅C to meet BC at point C'.

9. Through C', draw a line parallel to side CA to meet BA at A'.

A'BC' is the required triangle.