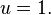CBSE Class 11-science Answered

where the constant

has the dimension of length. Then

and

Differentiation with respect to time is transformed into differentiation with respect to angle:

Differentiate

twice:

Substitute into the radial equation of motion

and get

Divide by the right hand side to get a simple non homogenous differntial equations for the orbit of the planet:

An obvious solution to this equation is the circular orbit

These solutions are

where and are arbitrary constants of integration. So the result is

Choosing the axis of the  coordinate system such that , and inserting , gives:

If this is the equation of an ellipse and illustrates Kepler's first law.

Only the tangential acceleration equation is needed to derive Kepler's second law.

The magnitude of the specific angular momentum

is a constant of motion , even if both the distance , and the angular speed , and the tangential velocity , vary, because

where the expression in the last parentheses vanishes due to the tangential acceleration equation.

The area swept out from time t₁ to time t₂,

depends only on the duration t₂ − t₁. This is Kepler's second law.

which is Kepler's third law for the special case.

In the general case of elliptical orbits, the derivation is more complicated.

The area of the planetary orbit ellipse is

The areal speed of the radius vector sweeping the orbit area is

where

The period of the orbit is

satisfying

implying Kepler's third law

Hope this helps.

Team

Topperelarning.com