CBSE Class 11-science Answered
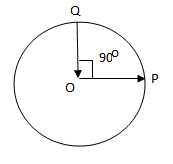
Can you please explain me how have we resolved v (rain,road) for the second diagram as
v(rain,road)sin(30°+a)=12km/h cos30° in detail ?

Asked by Varsneya Srinivas | 12 May, 2017, 04:31: PM
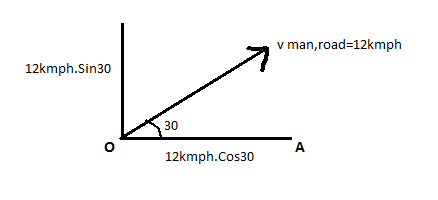
- Taking the components along OA indicates that OA has to be taken as a base reference to resolve the forces around it which are mentioned in equation (i).
- When OA is taken as a base reference, it is found that by the geometry of the velocity v man,road=2kmph, OA happens to be the horizontal component of this velocity.
- Therefore, OA=12kmph.Cos30.
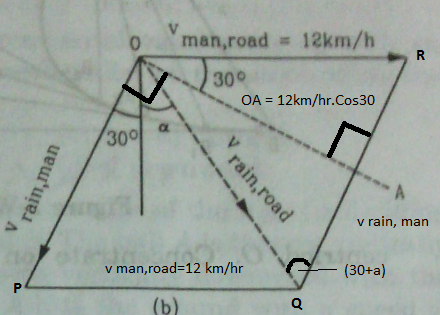
- Let the quadrilateral in the above diagram be parallelogram OPQR.
- In triangle OQA, angle Q=(30+a) as angle Q and angle (30+a) are the alternate angles formed between two parallel sides OP and RQ.
- Now by applying trigonometry in triangle OQA

- This is how we get equation (iii) of the solution mentioned in your query.
Answered by Abhijeet Mishra | 14 May, 2017, 12:44: PM
Concept Videos
CBSE 11-science - Physics
in a vertical circle of radius r at what point in its path a particle may have tension equal to zero
Asked by momintaufik26 | 13 Oct, 2023, 08:26: PM
CBSE 11-science - Physics
Asked by anshujaiswalname | 10 Sep, 2023, 01:29: PM
CBSE 11-science - Physics
Asked by subhashreeojha235 | 20 Jul, 2023, 11:22: AM
CBSE 11-science - Physics
Asked by advssdrall | 07 Oct, 2022, 11:11: PM
CBSE 11-science - Physics
Asked by sohail.saba0311 | 09 Sep, 2021, 08:23: PM
CBSE 11-science - Physics
Asked by ananthi.baskae | 07 Sep, 2021, 09:18: AM
CBSE 11-science - Physics
Asked by udityashekhawat123 | 09 May, 2020, 12:26: AM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM





 .
At what instant the velocity vector will make an angle 45o with X-axis.
.
At what instant the velocity vector will make an angle 45o with X-axis.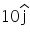 m/s and moves in XY plane with a constant acceleration of
m/s and moves in XY plane with a constant acceleration of 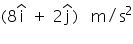 .
(a) At what time is the X-coordinate of the particle 16 m?
(b) What is the Y-coordinate of the particle at that time?
.
(a) At what time is the X-coordinate of the particle 16 m?
(b) What is the Y-coordinate of the particle at that time?