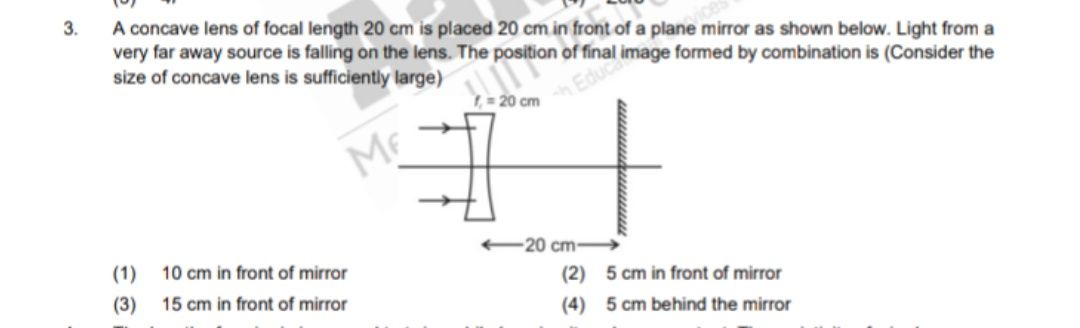
CBSE Class 10 Answered

Object distance, u = +12 cm (virtual object)
 
(a) Focal length of the convex lens, f = 20 cm
     Image distance = v
     Applying lens formula 
     1/v – 1/u = 1/f
       1/v =  1/u+ 1/f
        1/v = 1/12  + 1/20
     Therefore putting the values and solving the equation, we get v = 60/8 i.e. = 7.5 cm
     Hence, the image is formed 7.5 cm away from the lens, toward its right.
(b) Focal length of the concave lens, f = -16
     again image distance = v
     Using lens formula
     1/v - 1/u = 1/f
      1/v = 1/u + 1/f
      1/v = 1/12 -1/16
     the again as previous, applying the lens formula, substituing the values of u and f, we get v= 48 cm.
     Hence, the image is formed 48 cm away from the lens, towards its right.