CBSE Class 9 Answered
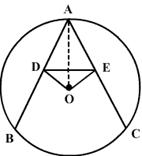
BE and CD are two equal chords of circle with centre O. These chords when produced meet at E. Prove that BE = ED .
Asked by Vikas | 11 Jan, 2018, 09:10: AM
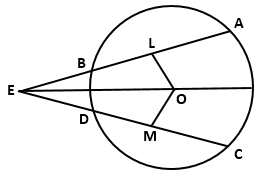

Answered by Rashmi Khot | 11 Jan, 2018, 10:24: AM
Concept Videos
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 9 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:15: AM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Aug, 2017, 08:51: AM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 9 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:17: AM
CBSE 9 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:25: AM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Aug, 2017, 08:49: AM
CBSE 9 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:22: AM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Aug, 2017, 08:40: AM
CBSE 9 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:24: AM




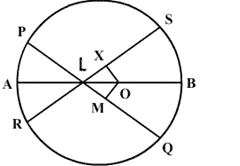
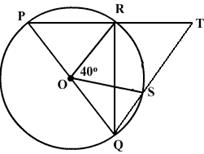
 XPZ is equal to twice the sum of
XPZ is equal to twice the sum of 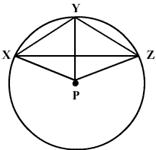
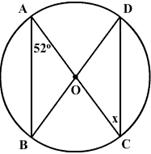
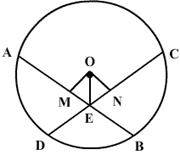
 ADE is an isosceles triangle.
ADE is an isosceles triangle.