Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is 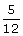. On walking 192 metres towards the tower, the tangent of the angle of elevation is 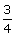. Find the height of the tower. OR The horizontal distance between two towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. The height of the second tower is 60 m find the height of the first tower.
Asked by Topperlearning User | 30 Nov, 2013, 02:13: AM
answered-by-expert Expert Answer

 

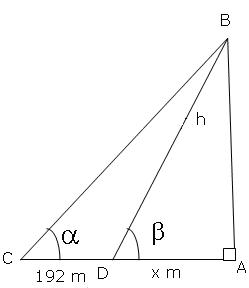
Let AB be the tower of height h metres. Let AD=x metres, CD=192 metres.

tanα = , tanβ =

In ∆BAC,

tanα = = ……………………. (i)

In ∆DAB,

tanβ = = or x= ……………………… (ii)

Using (ii) in (i)

=

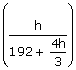
5= 12h

2880 +20h =36h

16h = 2880 or h= 180

Hence, the height of the tower is 180 metres.

OR

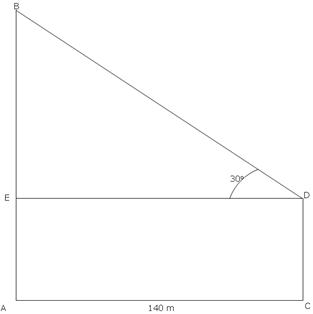
Let AB and CD be two towers of height h m and 60 m respectively.

AC=140m and ÐBDE =300.

In ∆DEB,

tan 30° =

 

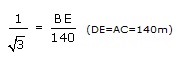
BE == 80.83m

Thus, the height of the first tower is

AB= AE+BE = CD+BE =60+80.83 = 140.83m

Answered by | 30 Nov, 2013, 04:13: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
Two pillars are standing on either side of a 80 m wide road. Height of one pillar is 20 m more than the height of the other pillar. From a point on the road between the pillars, the angle of elevation of the higher pillar is 60°, whereas that of the other pillar is 30°. Find the position of the point between the pillars and the height of each pillar. (Use √3 = 1-73)
Asked by swetalinasamantaray022 | 21 Mar, 2023, 04:15: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
On a warm and lazy Saturday, Rishi is watching a county maintenance crew mow the park across the street. He notices the mower takes 16 sec to pass through 60c of rotation from one end of the park to the other. If the corner of the park is 40 meter directly across the street from his house,  (i) How wide is the park?  (ii) How fast (in kmph) does the mower travel as it cuts the grass?
Asked by badakhsharda | 14 Apr, 2022, 08:57: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is √st.
Asked by naancysingh | 09 Apr, 2022, 07:07: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
a person standing on the bank of a river observes that the angle subtented by a tree on the opposite bank of 60 degree. when he retreates 20m from the bank he find the angle to be 30 degree . find the height of the tree and the bradth of the river
Asked by vy499292 | 23 Jan, 2022, 08:04: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
If two crows are sitting at a height of 15 m and 10 m on different trees vertically opposite to each other. They view a vaddi (an estable) on the ground at a angle of depression 45°and 60° respectively. They start at the same time and fly at the same speed along the shortest path to pick up the vadai.Which bird will succeed in it.?
Asked by urzashu7818 | 15 Jan, 2021, 12:52: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
question
question image
Asked by arindeep.singh | 02 Oct, 2020, 12:19: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
question
question image
Asked by arindeep.singh | 02 Oct, 2020, 12:19: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
the angle of elevation of a cloud from a point h metre above a lake is theta. the angle of depression of its reflection in the lake is 45 degree. Find the height of the cloud
Asked by arindeep.singh | 11 Sep, 2020, 02:41: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
a fire in the building Bis reported on telephone to two fire staitons P and Q, 20 km apart from each other on a straight road P observes that the fire is at an angle of 60 degree to the road and Q observes that it is at an angle of 45 degree to the road. What station should send its team and how much time will this team have to travel?
Asked by debeswar32 | 06 Aug, 2020, 10:55: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
from a point on the ground the angles of elevation of the bottom and top of a communication tower fixed on the top of a 20 meter high building a 45 degree and 60 degree respectivelyf.find the height of the tower.
Asked by ahmadaarif199 | 24 Jul, 2020, 02:58: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×