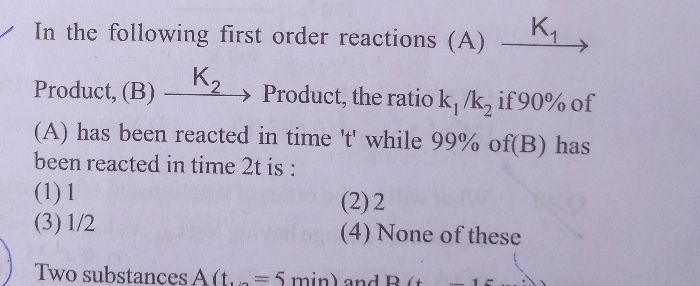CBSE Class 12-science Answered

Method of Initial Rates

When looking at the expression for the , you should notice that the variables in the equation are the concentration terms and the powers p and q:

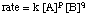
Because we can measure the concentrations in the rate law using the techniques described above, the unknowns we wish to measure are k, p, and q. One method of directly measuring k, p, and q is called the method of initial rates. By measuring the initial rate (the rate near reaction time zero) for a series of reactions with varying concentrations, we can deduce to what power the rate depends on the concentration of each reagent. For example, let's use the method of initial rates to determine the rate law for the following reaction:

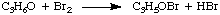
whose rate law has the form:

Using the following initial rates data, it is possible to calculate the order of the reaction for both bromine and acetone:

Figure %: Initial rates data for the bromination of acetone

To calculate the order of the reaction for bromine, notice that experiments 1 and 2 hold the concentration of acetone constant while doubling the concentration of bromine. The initial rate of the reaction is unaffected by the increase in bromine concentration, so the reaction is zero order in bromine. We can prove this mathematically by taking the ratio of the rates from experiments 1 and two:

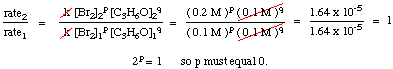
As you can see in the above equations, by holding the concentrations of all but one species constant between two experiments, you can calculate the order of the reaction in a single reactant at a time. By similar reasoning, we can conclude that because the rate of reaction doubled when the concentration of acetone was doubled (cf. experiments 1 and 3) the reaction must be first order in acetone. However, had the rate quadrupled or octupled with a doubling of the acetone concentration, the reaction would have been second or third order in acetone, respectively. In practice, you will likely never see a reaction with an order higher than 3. If you calculate an order higher than 3 for a reaction, double check your math because that is highly unusual. If you compute a fractional power for a reactant's order, do not be discouraged; they are quite common (especially half-order reactions).

To calculate the value of k, the rate constant, you simply plug into the rate law the values of the concentrations, the orders, and the rate of the reaction from any one of the three experiments. All three experiments should give a value of 1.64 x 10^-4 s^-1. You should prove this to yourself.