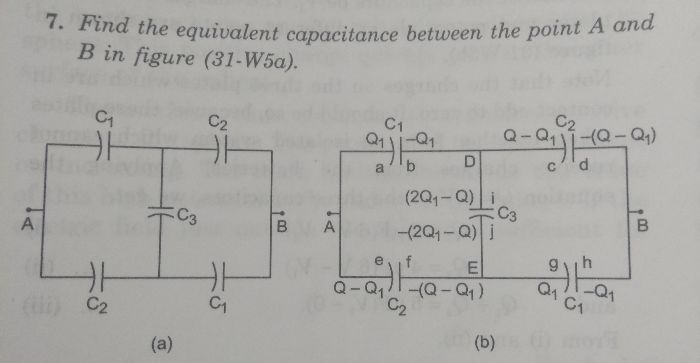
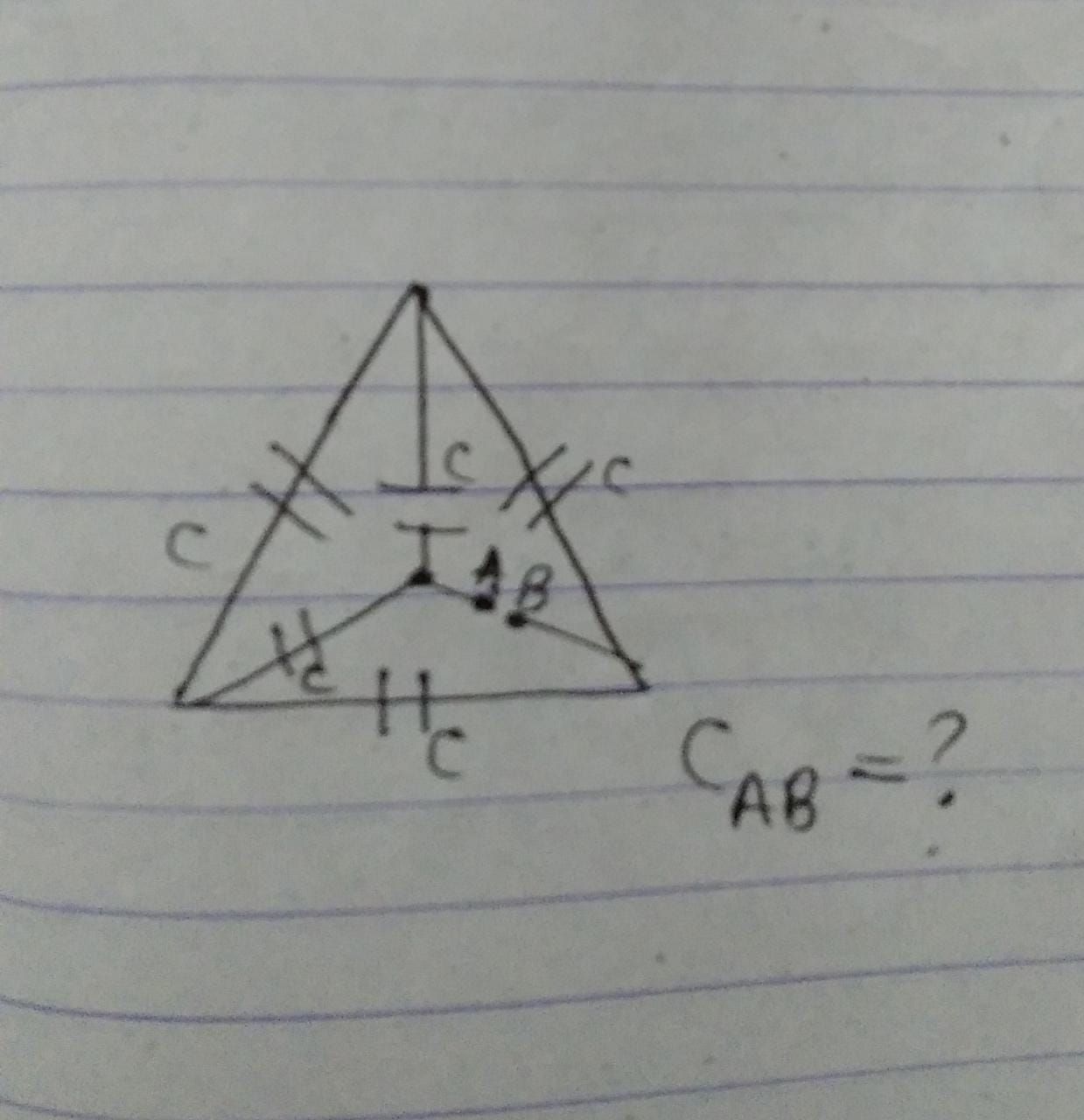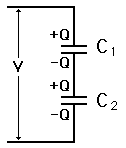CBSE Class 12-science Answered
Answer fast

Asked by Varsneya Srinivas | 07 Jan, 2018, 09:54: PM
Charge as a function of time on the capacitor of capacitance C while charging is given by
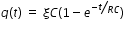
ξ is emf of the battery. After long time capacitor is charged its full charge, Q = ξC.
Let time taken for charging half of Q is th, then 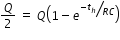
Solving for th we will get th = (ln2)RC
Energy dissipated dE in resistor while charging for a time dt is given by dE = i2Rdt
Where i is the current as a function of time is given by 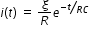
Hence 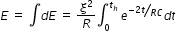
To solve the above integration, let τ = (2t)/RC, then dt = (RC/2)dτ, limits t=0 -> τ=0 and t=th -> τ = ln4
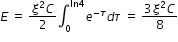
Answered by Thiyagarajan K | 09 Jan, 2018, 02:13: PM
Concept Videos
CBSE 12-science - Physics
Asked by sunil07011988 | 28 Jun, 2020, 12:49: PM
CBSE 12-science - Physics
Asked by arss9101127 | 11 May, 2020, 08:56: AM
CBSE 12-science - Physics
Asked by Shaikmustaqeem007 | 27 Jan, 2020, 11:34: PM
CBSE 12-science - Physics
Asked by Topperlearning User | 22 Apr, 2015, 10:57: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 22 Apr, 2015, 10:59: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 22 Apr, 2015, 10:59: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 22 Apr, 2015, 11:00: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 22 Apr, 2015, 11:01: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 22 Apr, 2015, 11:04: AM