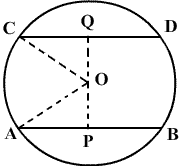
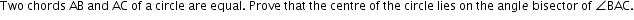CBSE Class 9 Answered
An isosceles triangle is inscribed in a circle. If AB=AC=12root5 cm and BC=24 cm, find the radius of the circle
Asked by adityaahuja099 | 02 Dec, 2017, 09:26: AM
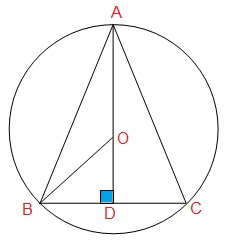

Answered by Arun | 02 Dec, 2017, 04:04: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by subbusuchi1978 | 05 Nov, 2023, 10:24: AM
CBSE 9 - Maths
Asked by rameshsonkar1234ramesh | 21 Dec, 2022, 11:03: PM
CBSE 9 - Maths
Asked by chalkekalyani80 | 06 Mar, 2022, 11:25: AM
CBSE 9 - Maths
Asked by tejvinder3r | 27 Jan, 2020, 10:27: AM
CBSE 9 - Maths
Asked by arvindhsb2005 | 14 Jan, 2020, 09:14: PM
CBSE 9 - Maths
Asked by sambitgenius2005 | 24 Apr, 2019, 08:03: PM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Aug, 2017, 09:07: AM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 9 - Maths
Asked by Topperlearning User | 14 Feb, 2014, 02:05: PM