CBSE Class 10 Answered

Theorem: If the tangent to a circle and the radius of the circle intersect they do so at right angles :

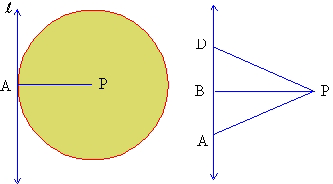
         Figure (a)              Figure (b)

In figure (a) l is a tangent to the circle at A and PA is the radius.

To prove that PA is perpendicular to l , assume that it is not.

Now, with reference to figure (b) drop a perpendicular from P onto l at say B. Let D be a point on l such that B is the midpoint of AD.

In figure (b) consider   PDB and   PAB

seg.BD congruent to seg.BA ( B is the midpoint of AD)

angle PBD = angle PBA ( PB is perpendicular to l ) and

triangle PBD congruent to triangle PAB (SAS)

seg.PD congruent to seg.PA corresponding sides of congruent triangles are congruent.

 D is definitely a point on the circle because l (seg.PD) = radius.

D is also on l which is the tangent. Thus l intersects the circle at two distinct points A and D. This contradicts the definition of a tangent.

Hence the assumption that PA is not perpendicular to l is false. Therefore PA is perpendicular to l.

Tangent Secant Theorem: If a chord intersects the tangent at the point of tangency, the angle it forms is half the measure of the intercepted arc. In the figure 1 l is tangent to the circle. Seg.AB which is a chord, intersects it at B which is the point of tangency.

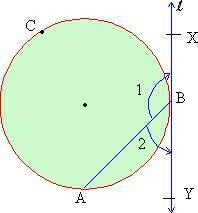
Figure 1

The angles formed angle ABX and angle ABY are half the measures of the arcs they intercept.

angle 1 = m (arc ACB)

angle 2 = m (arc AB)

This can be proved by considering the three following cases.

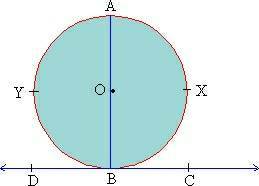
Figure 2

O is the center of the circle

Arc AXB can be

a) Semi circle

b) minor arc

c) major arc

Case 1 : Assume arc AXB is a semicircle when angle ABC intercepts a semicircle the chord AB passes through the center. Therefore angle ABC = 90⁰ (a tangent is always perpendicular to the diameter that intersects it at the point of tangency).

 (arc BXA) = 180⁰ (arc BXA is a semi circle)

(arc BXA) = ´ 180⁰ = 90⁰

angle ABC = (arc BXA)

Case 2 : Assume that angle ABC intercepts a minor arc. Therefore as seen in figure 3 the center O lies in the exterior of angle ABC.

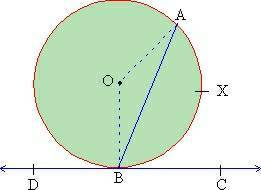
Figure 3

angle ABC = 90⁰ - angle ABO

angle ABO = 90⁰ - angle ABC ----------- (1)

But angle ABO = angle OAB

(as OAB is an isosceles triangle )

angle OAB = 90⁰ - angle ABC ----------- (2)

(1) + (2)

angle ABO + angle OAB = 180 - 2 angle ABC

Since angle ABO + angle OAB = 180 - angle BOA

180 - angle BOA = 180 - 2 angle ABC

i.e. angle BOA = 2 angle ABC

angle ABC = angle BOA

angle ABC =   ( arc AXB )

Case 3 :

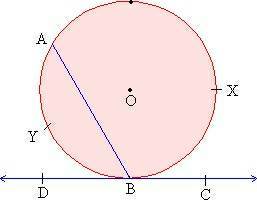
Figure 4

If angle ABC intercepts a major arc, the center of the circle O will lie in the interior as angle ABC . See figure 4.

Now angle ADB intercepts a minor arc AYB.

angle AOB =  (arc AYB)

180⁰ - angle ADB = { 360⁰ -  (arc AXB) }

180⁰ - angle ADB = 180⁰ -   (arc AXB)

angle ADB =   (arc AXB)