Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 9 Answered

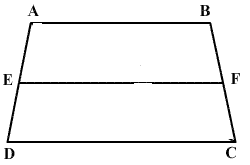
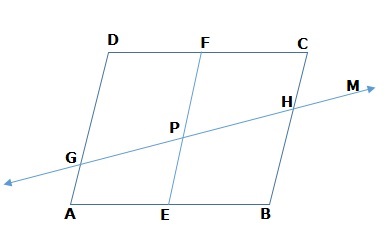
ABCD is a parallelogram. E and F are the midpoints of AB and CD respectively. GM is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP = PH

Asked by Paresh | 11 Dec, 2015, 02:56: PM
answered-by-expert Expert Answer
C o n s i d e r space t h e space f o l l o w i n g space f i g u r e.
A B C D space i s space a space p a r a l l e log r a m comma space E space a n d space F space a r e space t h e space m i d p o i n t s space o f space t h e space s i d e s space A B space a n d space C D space r e s p e c t i v e l y. T h e r e f o r e comma space A D parallel to E F parallel to B C T h e space l i n e space G M space i n t e r s e c t s space t h e space l i n e space s e g m e n t s space A D comma space E F space a n d space B C space a t space G comma space P space a n d space H space r e s p e c t i v e l y. W e space n e e d space t o space p r o v e space t h a t space G P equals P H I f space t h r e e space o r space m o r e space p a r a l l e l space l i n e s space i n t e r s e c t space a space t r a n s v e r s a l comma space t h e n space t h e y space c u t space o f f space t h e space t r a n s v e r s a l space p r o p o r t i o n a l l y. H e r e comma space A D comma space E F space a n d space B C space a r e space t h r e e space p a r a l l e l space l i n e s space a n d space G H space i s space t h e space t r a n s v e r s a l. therefore fraction numerator A E over denominator E B end fraction equals fraction numerator C F over denominator D F end fraction equals fraction numerator G P over denominator P H end fraction S i n c e space E space a n d space F space a r e space m i d p o i n t s space o f space A B space a n d space C D space r e s p e c t i v e l y comma space w e space h a v e comma A E equals E B space a n d space C F equals D F rightwards double arrow fraction numerator G P over denominator P H end fraction equals 1 rightwards double arrow G P equals P H
Answered by Vimala Ramamurthy | 12 Dec, 2015, 12:49: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 9 - Maths
the line segment joining the midpoints of two sides of a triangle is parallel to the third side
Asked by vineetyadav77050 | 25 Jul, 2021, 05:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Q. 7
question image
Asked by Rayeesa | 04 Jun, 2018, 09:58: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
M is the mid point of side PQ of a parallelogram PQRS. A line through Q parallel to PS meets SR at N and PS produced at L. Prove that (i) PL = 2QR (ii) QL = 2QN.
Asked by Topperlearning User | 11 Aug, 2017, 11:58: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
State the mid point Theorem.
Asked by Topperlearning User | 11 Aug, 2017, 12:01: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that the triangles formed by joining in pairs, the mid points of the three sides of a triangle are congruent to each other.
Asked by Topperlearning User | 11 Aug, 2017, 11:59: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that the line drawn through the mid point of one side of a triangle, parallel to another side, intersects the third side at its mid point.
Asked by Topperlearning User | 11 Aug, 2017, 12:00: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
In PQR, A, B and C are the mid points of QR, RP and PQ respectively. If the lengths of sides PQ, QR and RP are 7 cm, 8 cm and 9 cm respectively, find the perimeter of ABC. 
Asked by Topperlearning User | 11 Aug, 2017, 12:00: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that the triangle formed by joining the mid points of the sides of an isosceles triangle is an isosceles triangle.
Asked by Topperlearning User | 11 Aug, 2017, 11:52: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
In the figure, E is the mid-point of side AD of a trapezium ABCD with AB  CD. A line through E parallel to AB meets BC in F. Show that F is the mid point of BC.
Asked by Topperlearning User | 11 Aug, 2017, 11:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
M, N and P are the mid points of AB, AC and BC respectively. If MN = 3 cm, NP = 3.5 cm and MP = 2.5 cm. Calculate BC, AB and AC.
Asked by Topperlearning User | 11 Aug, 2017, 11:59: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×