Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 9 Answered

ABC is an acute angled triangle and CD be the altitude through C. If AB = 6 cm and CD = 8 cm, then find the distance between mid-points of AD and BC.
Asked by a.behera67 | 02 Jan, 2016, 09:19: PM
answered-by-expert Expert Answer
 
Let space straight P space and space straight Q space be space the space midpoints space of space AD space and space BC. Draw space QR space perpendicular space to space AB. In space increment BDC space and space increment BRQ angle straight D space equals space angle straight R space equals 90 degree angle straight B equals angle straight B therefore increment BDC space almost equal to space increment BRQ space left parenthesis AA space test space of space similarity right parenthesis Using space converse space of space BPT space theorem space we space can space say space that comma space since space straight Q space is space midpoint space of space BC space so space straight R space is space midpoint space of space BD. straight P space is space midpoint space of space AD space and space straight R space is space midpoint space of space DB AP plus RB equals PD plus DR space space left parenthesis because RB space equals space DR space and space AP space equals space PD right parenthesis therefore PR space equals 1 half AB equals 4 Also comma QR space equals 1 half CD equals 3 space open parentheses because increment BDC space almost equal to space increment BRQ space and space using space BPT space theorem space close parentheses therefore Applting space pythagorean space triplet space 3 minus 4 minus 5 space PQ space must space be space space 5 space unnits.
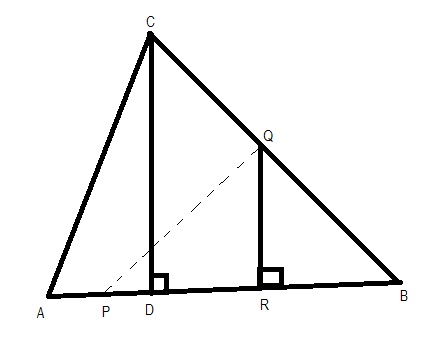
Answered by Vijaykumar Wani | 04 Jan, 2016, 10:48: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 9 - Maths
area of right triangle is 240cm and side other than hypotenuse is 30cm.find the perimeter
Asked by bascaljoseph | 07 Feb, 2023, 01:27: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
find the percentage increase in the area of the triangle if it side is doubled
Asked by deepakumaraiya200 | 30 Jun, 2020, 09:51: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
an isosceles right angled triangle has an area of 8cm square.find the lenght of its hypotenuse.
Asked by kishor.kp14 | 15 Dec, 2019, 05:00: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
The sides of a triangular plot are in the ratio of 3:5:7 and it's perimeter is300 meter .find its area
Asked by ravinderchoudhary0486 | 06 Dec, 2019, 10:59: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
The sides of triangular park in ratio of 2:6:7 and it perimeter is 300m.  Then its area is   
Asked by kumarvsteel477 | 12 Sep, 2019, 08:22: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Find the area of an isosceles triangle whose perimeter is 60cm and each of equal sides is 24cm  
Asked by phukansayan5 | 28 Aug, 2019, 06:16: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
If the area of an equilateral triangle is 16√3cmsq then find the perimeter of the triangle 
Asked by arunpssac | 19 Aug, 2019, 07:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
the base of a triangular field is three times its altitude is the cost of sowing the field at rupees 58 per hectare is rupees 783 find its base and height   
Asked by yuvrajlkr8877 | 07 Aug, 2019, 09:31: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
A piece of paper is in the shape of a right-angled triangle and is cut along a line that is parallel to the hypotenuse, leaving a smaller triangle. There was 35% reduction in the length of the hypotenuse of the triangle. If the area of the original triangle was 34 square inches before the cut, what is the area (in square inches) of the smaller triangle?
Asked by rushabhjain.av | 01 Apr, 2019, 07:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that a median divides a triangle into two triangle of equal area        
Asked by bhardwajvishesh2004 | 28 Nov, 2018, 04:18: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×