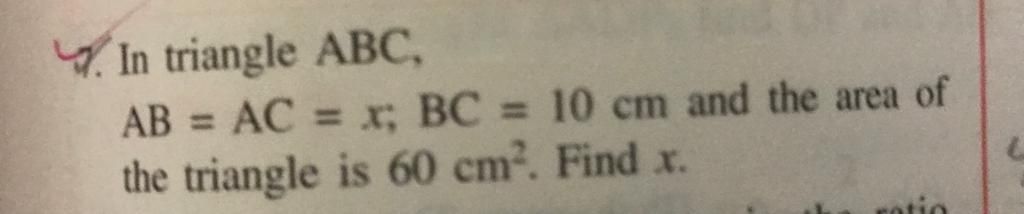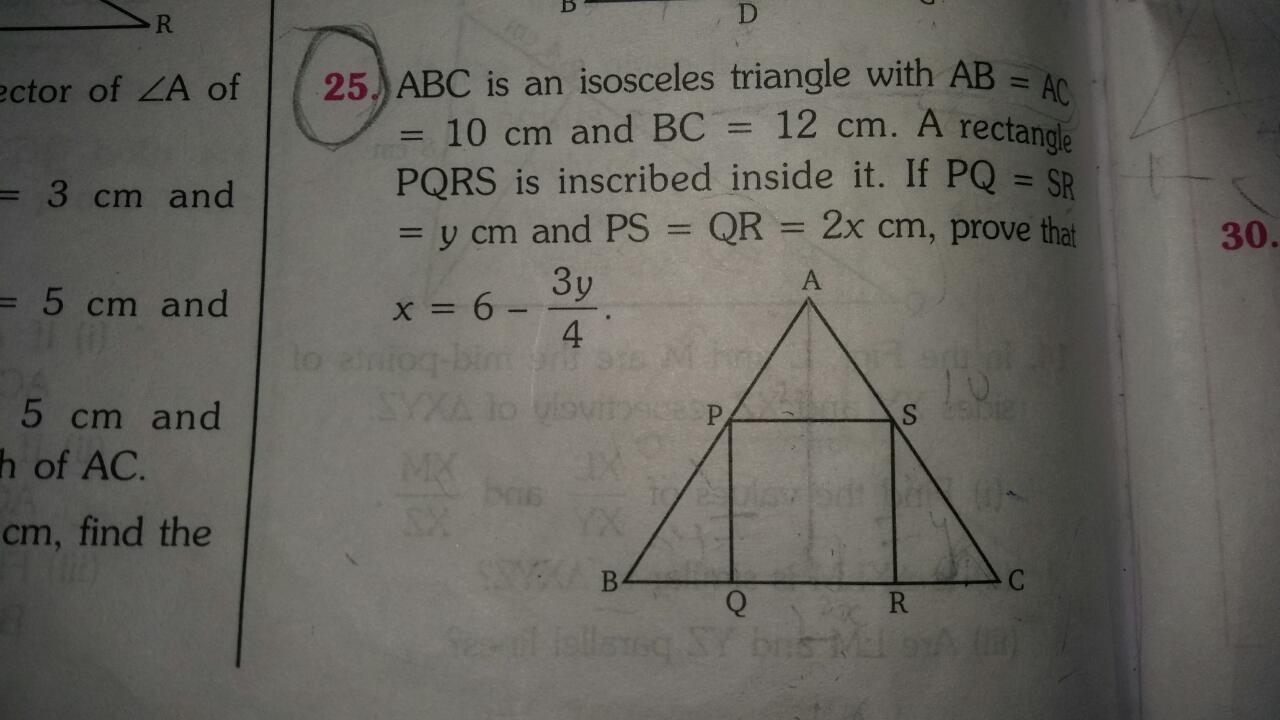ICSE Class 9 Answered
ABC is a right angled triangle in which ∠ABC = 90° and ∠ACB = 60°. BC is produced to D such that ∠ADB = 45°. If CD = 30 cm, what are the lengths of AB and BC?
Asked by akifmohd007 | 03 Jan, 2020, 12:06: PM
ABC is a right angled triangle such that right angled at B and angle ACB is 60o. BC is produced to D such that angle ADB is 45o and CD is 30 cm.
To find the lengths of AB and BC.
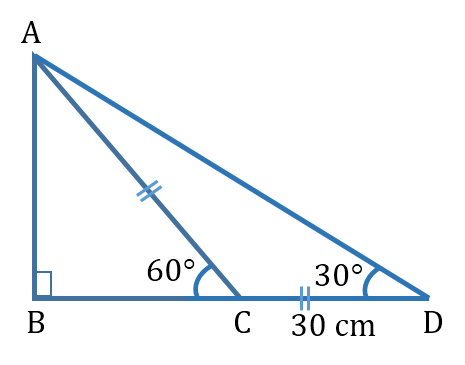

Answered by Renu Varma | 07 Jan, 2020, 10:50: AM
Application Videos
Concept Videos
ICSE 9 - Maths
Asked by mak121007abk | 25 Feb, 2023, 07:39: PM
ICSE 9 - Maths
Asked by aryan2mumbai | 01 Sep, 2020, 08:29: PM
ICSE 9 - Maths
Asked by kavyaraval1075.9sdatl | 08 Jun, 2020, 07:35: PM
ICSE 9 - Maths
Asked by simranmangnani2282.9sdatl | 13 May, 2020, 02:52: PM
ICSE 9 - Maths
Asked by akifmohd007 | 03 Jan, 2020, 12:06: PM
ICSE 9 - Maths
Asked by kadtej83 | 24 Jan, 2019, 05:37: AM
ICSE 9 - Maths
Asked by bsap6777 | 28 Aug, 2018, 09:50: PM
ICSE 9 - Maths
Asked by Sunita | 09 Mar, 2018, 02:53: PM
ICSE 9 - Maths
Asked by Sunita | 09 Mar, 2018, 02:40: PM