ICSE Class 9 Answered
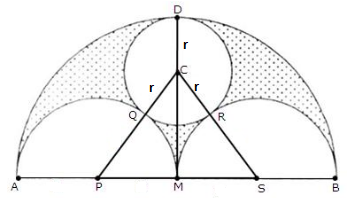
AB is a line segment whose midpoint is M. Taking AM, BM and AB as diameters three semi-circles are drawn on the same side of AB. A circle is drawn with radius 'r' touching all the three semi-circles. Prove that r=AB/6
Asked by abhishekabin12306 | 03 Jan, 2018, 08:01: PM
The image will be as shown below:

Answered by Rashmi Khot | 05 Jan, 2018, 10:22: AM
Application Videos
Concept Videos
ICSE 9 - Maths
Asked by mdrehanagrawal | 20 Nov, 2020, 04:40: PM
ICSE 9 - Maths
Asked by anshu8958660720 | 18 Oct, 2020, 11:57: AM
ICSE 9 - Maths
Asked by nityamcgsmehta | 31 Oct, 2019, 12:31: PM
ICSE 9 - Maths
Asked by pachusa.2 | 26 Mar, 2019, 07:31: PM
ICSE 9 - Maths
Asked by Dimple | 10 Jan, 2018, 08:26: PM
ICSE 9 - Maths
Asked by dhruvassaravana | 09 Jan, 2018, 10:18: PM
ICSE 9 - Maths
Asked by abhishekabin12306 | 03 Jan, 2018, 08:01: PM