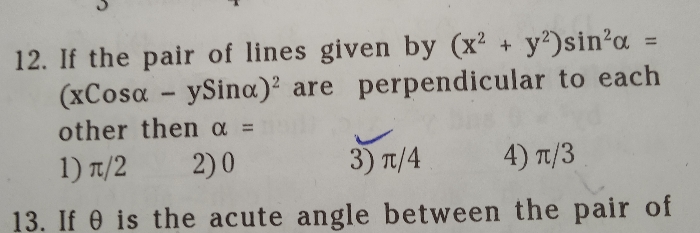Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

AB is a line of fixed length, 6 units, joining the points A(t,0) and B which lies on thepositive y axis. P is a point on AB distant 2 units from A. Express the coordinates of B and P in terms of t. Find the locus of P as t varies.
Asked by kandappan | 13 Feb, 2020, 01:39: PM
answered-by-expert Expert Answer
AB is a line segment of length 6 units where A is (t, 0) and B lies on the positive y-axis
Let B be (0, k) and the coordinates of P be (x, y)
As it is given that P is at a distance of 2 from A and lies on AB
Therefore, AP = 2 and PB = 4
So, we can say P divides the line segment AB in the ratio 1 : 2
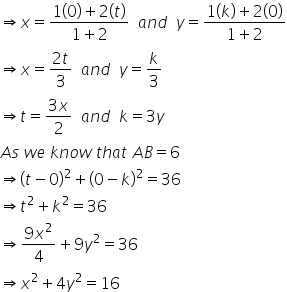
rightwards double arrow x equals fraction numerator 1 left parenthesis 0 right parenthesis plus 2 left parenthesis t right parenthesis over denominator 1 plus 2 end fraction space space a n d space space y equals fraction numerator 1 left parenthesis k right parenthesis plus 2 left parenthesis 0 right parenthesis over denominator 1 plus 2 end fraction rightwards double arrow x equals fraction numerator 2 t over denominator 3 end fraction space space a n d space space y equals k over 3 rightwards double arrow t equals fraction numerator 3 x over denominator 2 end fraction space space a n d space space k equals 3 y A s space w e space k n o w space t h a t space A B equals 6 rightwards double arrow open parentheses t minus 0 close parentheses squared plus open parentheses 0 minus k close parentheses squared equals 36 rightwards double arrow t squared plus k squared equals 36 rightwards double arrow fraction numerator 9 x squared over denominator 4 end fraction plus 9 y squared equals 36 rightwards double arrow x squared plus 4 y squared equals 16
Answered by Renu Varma | 14 Feb, 2020, 11:52: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Maths
program to find the minimum element from a list of element along with its index in the list
question image
Asked by sampabarman328 | 18 Apr, 2024, 01:20: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
find square root of 7+24i
Asked by tahikpreet0001 | 17 Apr, 2024, 06:41: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
if α, ß, Γ be the roots of the equation x^3+px^2+qx+r=0 then find the value of (α+ß-3Γ)(ß+Γ-3α)(α+Γ-3ß)
Asked by nitinkrjsr07082008 | 15 Apr, 2024, 11:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
ug
question image
Asked by nityaboragam | 11 Apr, 2024, 12:14: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
total number of three letter words formed using all the letters of the word "SHINE" is
Asked by kanhaparashar17 | 04 Apr, 2024, 12:55: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
find 6th term from and of the (x-1/x)⁹
Asked by dseno1741 | 29 Mar, 2024, 08:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
in exercise 1.3 1st q ii part abc is not subset of bcd but two elements are common i.e bc but in 2 question same exercise i part ab is subset of  bca how ??  
Asked by parvanipatil09 | 29 Mar, 2024, 10:12: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
find the value of x so that the vectors are (2,7,5) ,(3,-3,6) ,(x,2,-5) may be coplanar
Asked by rishithatelaprolu84 | 29 Mar, 2024, 08:32: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
binomial doubt
question image
Asked by Manjeet | 23 Mar, 2024, 09:41: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
pair
question image
Asked by rambabum3372 | 21 Mar, 2024, 04:51: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×