Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

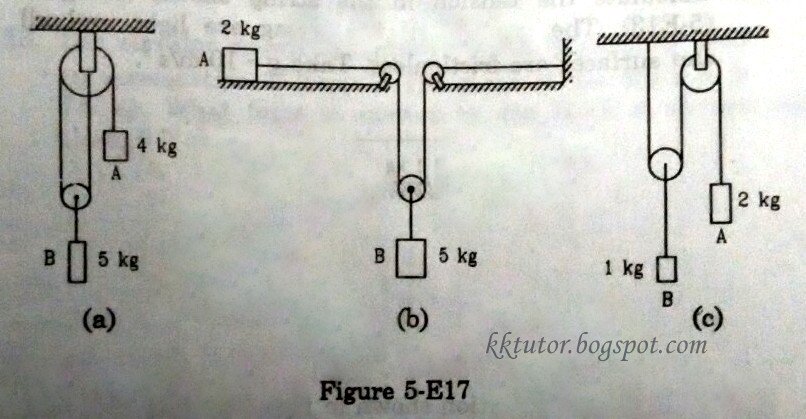
CBSE Class 11-science Answered

A uniform chain of length l and mass m lies on a smooth table. A very small part of this chain hangs from the table. It begins to fall under the weight of hanging end. Find the velocity of chain when the length of hanging part becomes y.
Asked by devanshu_jain | 19 Oct, 2010, 07:21: PM
answered-by-expert Expert Answer

Dear Student,

Let d = mass per length = m/l

When length of hanging part is y, the velocity = v    . . (I)

Table surface is frictionless.

Kinetic energy at (I) =  1/2 mv2 = Loss of potential energy.

Loss of potential energy =  d*y*g*y/2           .  .  . (dygy - dygy/2)

(centre of mass of hanging chain is at y/2)

Hence

1/2 mv2  =  m/l * y2 * g/2

v2  =  g * y2/ l

v   =  y √(g/l)

We hope that clarifies your query.
Regards
Team
Topperlearning

Answered by | 22 Oct, 2010, 01:32: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Physics
Can you tell an example about a body having 0 velocity and still accelerating?
Asked by veenasangeeth2020 | 30 Jan, 2024, 09:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
mention the expression for work done
Asked by abdulkhadirchajjo549 | 06 Dec, 2023, 06:55: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
During calculation of acceleration due to gravity above the surface of earth if we assume that there is an external force opposite to that of Earth's gravity then the cos angle will be 180 between the two forces which is negative(-1), if we put the value in the equation of dw = F.dx then the final value of potential energy is positive which is not possible.how and why??
Asked by anushkaverma.25707 | 24 Aug, 2023, 07:35: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
In the problem no. 34 of concepts of physics HC Verma-1 bit(a) , why is the acceleration of block B is half the acceleration of block A? And why is it that distance travelled by block B is half the distance travelled by block A?
question image
Asked by sakethrockzz007 | 04 Aug, 2023, 11:17: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
A small spherical object having density 2P is placed inside the liquid of density P and connected to an ideal string of length l whose other end is kept fixed so that the object can move in a vertical cirlcle, minimum speed which must be given at the bottom to just complete the vertical circle.
Asked by dhruvund8769 | 04 Feb, 2023, 11:41: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
For a liquid drop of radius r falling in air with terminal velocity power delivered by gravitational force is proportional to
Asked by gdeadshot85 | 12 Jan, 2023, 10:28: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
when we push the car,workdineyis 0,how
Asked by vaniimtiyaz630 | 12 May, 2022, 12:19: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
Two identical balls moving in opposite directions with speeds 20m/s and 25m/s undergo head on perfectly inelastic collision. The speed of combined mass after collision is 1. 20m/s 2. 22.5m/s 3. 25m/s 4. 2.5m/s
Asked by KRISHPATEL.soc | 22 Apr, 2022, 04:19: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
explain about conservation of energy with problem
Asked by bandarirohinipriya | 08 Feb, 2022, 09:46: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
Derive expression for final velocity after perfectly inelastic collision  
Asked by unnatibhise08 | 22 Dec, 2021, 08:46: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×